
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 364 Дорофеев, Суворова — Подробные Ответы
Для каждой из функций и укажите соответствующий графику, если:
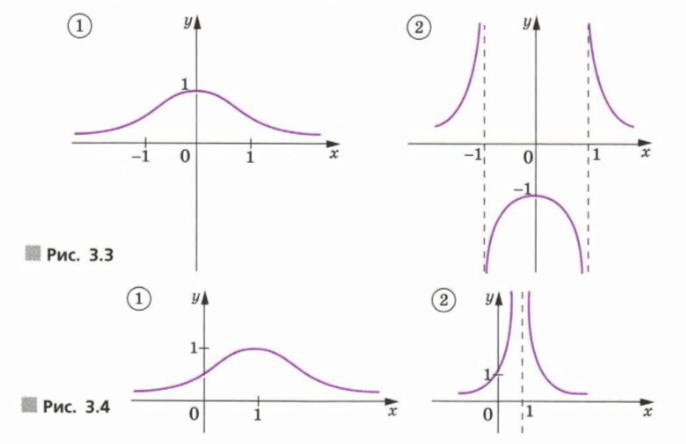
а) , (рис. 3.3);
б) , (рис. 3.4).
а) ;
Не имеет смысла при:
;
, отсюда ;
Соответствует графику 2;
;
Не имеет смысла при:
;
— корней нет;
Соответствует графику 1;
б) ;
Не имеет смысла при:
;
;
, значит корней нет;
Соответствует графику 1;
;
Не имеет смысла при:
;
, тогда:
;
Соответствует графику 2.
а)
Рассмотрим выражение в знаменателе функции , то есть .
Для нахождения области определения необходимо исключить из множества значений те значения переменной , при которых знаменатель обращается в ноль, так как деление на ноль не определено:
Найдём значения, при которых знаменатель равен нулю:
Решим уравнение:
Следовательно, функция не определена при и . При всех других значениях выражение имеет смысл. Это означает, что вертикальные асимптоты (прямые, к которым график стремится, но не пересекает) будут на прямых:
График функции имеет две точки разрыва, которые можно определить по нулям знаменателя. Следовательно, график функции разорван в этих точках, и именно они указывают на вертикальные асимптоты.
Соответствует графику №2, так как только он имеет асимптоты при , а график симметричен относительно оси , так как , то есть функция чётная.
Рассмотрим выражение в знаменателе .
Найдём, при каких значениях выражение не определено, то есть:
Решим уравнение:
Это уравнение не имеет действительных решений, поскольку квадрат любого действительного числа не может быть отрицательным. Таким образом, знаменатель никогда не обращается в ноль, и выражение определено при всех действительных значениях переменной .
Функция определена на всей числовой прямой и не имеет разрывов, то есть её график не содержит вертикальных асимптот. Кроме того, функция чётная, так как:
Соответствует графику №1, поскольку он не имеет асимптот и симметричен относительно оси .
б)
Рассмотрим выражение в знаменателе .
Найдём дискриминант квадратного выражения:
Дискриминант меньше нуля, значит квадратный трёхчлен не имеет действительных корней, и, следовательно, выражение в знаменателе не обращается в ноль ни при каких значениях .
Следовательно, функция определена при всех значениях , и её график не имеет вертикальных асимптот.
Кроме того, знаменатель всегда положителен:
Соответствует графику №1.
Рассмотрим выражение в знаменателе:
Найдём, при каких значениях переменной выражение не определено:
Следовательно, функция не определена при , и её график имеет вертикальную асимптоту в этой точке.
При всех остальных значениях функция определена. Так как выражение в знаменателе является квадратом, знак выражения в знаменателе всегда положителен при . Это означает, что график не меняет знака (функция положительна всюду, кроме разрыва).
Функция не является чётной, так как:
Соответствует графику №2, так как он имеет вертикальную асимптоту при , и график расположен только в положительной области .




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!