ГДЗ по Алгебре 9 Класс Номер 363 Дорофеев, Суворова — Подробные Ответы

На рисунке 3.2 изображены гиперболы — графики функций $y = \frac{1}{x}$, $y = \frac{1}{x — 1}$, $y = \frac{1}{x + 1}$.

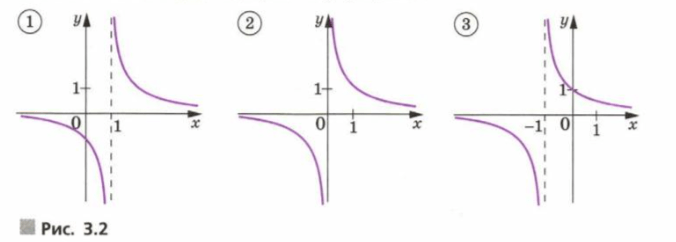
Уравнение вертикальной асимптоты гиперболы описывает значение аргумента, при котором функция не имеет смысла;

$y = \frac{1}{x}$;

Не имеет смысла при: $x = 0$;

Соответствует графику 2;

$y = \frac{1}{x — 1}$;

Не имеет смысла при:
$x — 1 = 0$, отсюда $x = 1$;

Соответствует графику 1;

$y = \frac{1}{x + 1}$;

Не имеет смысла при:
$x + 1 = 0$, отсюда $x = -1$;

Соответствует графику 3;

Уравнение вертикальной асимптоты гиперболы описывает те значения аргумента $x$, при которых знаменатель дроби становится равным нулю. В таких точках значение функции не определено, так как деление на ноль невозможно. Следовательно, в этих точках график функции имеет вертикальную асимптоту — прямую, к которой график бесконечно приближается, но не пересекает её и не принимает в ней значения.

Рассмотрим каждую из трёх функций:

$y = \frac{1}{x}$

Знаменатель выражения — это $x$. Функция не имеет смысла при $x = 0$, потому что тогда $y = \frac{1}{0}$, а деление на ноль невозможно. Следовательно, вертикальная асимптота — прямая $x = 0$. График с такой асимптотой соответствует графику 2, так как только на нём гипербола симметрична относительно начала координат, а асимптота проходит по оси $x = 0$.

$y = \frac{1}{x — 1}$

Знаменатель дроби — это $x — 1$. Приравниваем знаменатель к нулю:
$x — 1 = 0 \Rightarrow x = 1$

Следовательно, функция не определена при $x = 1$, а вертикальная асимптота проходит по прямой $x = 1$. Это означает, что график стремится к бесконечности при приближении к $x = 1$ слева и справа. График с этой асимптотой соответствует графику 1.

$y = \frac{1}{x + 1}$

Знаменатель дроби — это $x + 1$. Приравниваем знаменатель к нулю:
$x + 1 = 0 \Rightarrow x = -1$

Это значит, что при $x = -1$ функция не имеет смысла. Таким образом, вертикальная асимптота проходит по прямой $x = -1$. На графике эта гипербола будет сдвинута влево на одну единицу по сравнению с гиперболой $y = \frac{1}{x}$. Соответствует графику 3.

Ответ:

• $y = \frac{1}{x}$: не определена при $x = 0$, вертикальная асимптота $x = 0$ — график 2.
• $y = \frac{1}{x — 1}$: не определена при $x = 1$, вертикальная асимптота $x = 1$ — график 1.
• $y = \frac{1}{x + 1}$: не определена при $x = -1$, вертикальная асимптота $x = -1$ — график 3.