ГДЗ по Алгебре 9 Класс Номер 338 Дорофеев, Суворова — Подробные Ответы

а) Найдите все значения коэффициента $b$, при которых квадратный трёхчлен $2x^2 + bx + 8$ принимает только положительные значения. Запишите пример такого квадратного трёхчлена.

б) Найдите все значения коэффициента $c$, при которых квадратный трёхчлен $cx^2 — 3x + 25c$ принимает только отрицательные значения. Запишите пример такого квадратного трёхчлена.

а) $2x^2 + bx + 8 > 0$:

$D = b^2 — 4 \cdot 2 \cdot 8 = b^2 — 64 = (b — 8)(b + 8);$

$a = 2 > 0$, значит ветви параболы направлены вверх, тогда нам требуется найти значения $b$, при которых график не пересекает ось $x$;

2) Уравнение $2x^2 + bx + 8$ не имеет решений при $D < 0$:
$(b — 8)(b + 8) < 0$;

3) Нули функции:
$b_1 — 8 = 0$, отсюда $b_1 = 8$;
$b_2 + 8 = 0$, отсюда $b_2 = -8$;

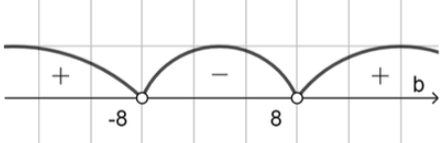
4) Значения на интервалах:

$b \in (-8; 8)$;

Пример такого трёхчлена: $2x^2 + 6x + 8$;

б) $cx^2 — 3x + 25c < 0$:

$D = 3^2 — 4 \cdot c \cdot 25c = 9 — 100c^2 = (3 — 10c)(3 + 10c);$

1) Ветви параболы направлены вниз при $c < 0$, нам требуется найти значения $c$, при которых график не пересекает ось $x$;

2) Уравнение $cx^2 — 3x + 25c$ не имеет решений при $D < 0$:
$(3 — 10c)(3 + 10c) < 0$;

3) Нули функции:
$3 — 10c_1 = 0$, отсюда $c_1 = 0{,}3$;
$3 + 10c_2 = 0$, отсюда $c_2 = -0{,}3$;

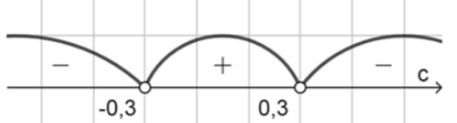
4) Значения на интервалах:

$c \in (-\infty; -0{,}3)$;

Пример такого трёхчлена: $-x^2 — 3x — 25$;

а) $2x^2 + bx + 8 > 0$:

Рассматриваем квадратный трёхчлен $2x^2 + bx + 8$. Необходимо определить, при каких значениях коэффициента $b$ этот трёхчлен принимает только положительные значения, то есть $> 0$ при любом $x \in \mathbb{R}$. Это означает, что график параболы находится полностью выше оси абсцисс, и, следовательно, не имеет точек пересечения с осью $x$.

Поскольку коэффициент при $x^2$ равен $2$, а это число положительное, значит, ветви параболы направлены вверх: $a = 2 > 0$. Чтобы парабола не пересекала ось $x$, дискриминант квадратного трёхчлена должен быть отрицательным: $D < 0$.

Вычислим дискриминант:

$D = b^2 — 4ac = b^2 — 4 \cdot 2 \cdot 8 = b^2 — 64$

Потребуем, чтобы дискриминант был меньше нуля:

$b^2 — 64 < 0$

Это неравенство можно преобразовать:

$b^2 < 64$

Решением этого неравенства являются значения $b$, лежащие внутри интервала:

$-8 < b < 8$

Таким образом, при любом значении $b$ из интервала от $-8$ до $8$ невключительно, квадратный трёхчлен будет принимать только положительные значения, так как его график — парабола, полностью лежащая выше оси абсцисс и не имеющая действительных корней.

Ответ: $b \in (-8; 8)$

Пример: при $b = 6$ получаем трёхчлен $2x^2 + 6x + 8$, который удовлетворяет условиям задачи.

б) $cx^2 — 3x + 25c < 0$:

Рассматриваем квадратный трёхчлен $cx^2 — 3x + 25c$. Требуется определить такие значения коэффициента $c$, при которых этот трёхчлен принимает только отрицательные значения, то есть $< 0$ при любом $x \in \mathbb{R}$.

Чтобы квадратный трёхчлен был всегда отрицательным, его график должен быть параболой, полностью лежащей ниже оси $x$, а значит:

Ветви параболы должны быть направлены вниз, то есть $a = c < 0$;

Парабола не должна пересекать ось $x$, то есть дискриминант уравнения должен быть отрицательным: $D < 0$.

Находим дискриминант:

$D = (-3)^2 — 4 \cdot c \cdot 25c = 9 — 100c^2$

Потребуем, чтобы:

$9 — 100c^2 < 0$

Решим это неравенство:

$-100c^2 < -9 \Rightarrow 100c^2 > 9 \Rightarrow c^2 > \frac{9}{100} \Rightarrow |c| > \frac{3}{10}$

С учётом условия $c < 0$ (ветви вниз), получаем:

$c < -\frac{3}{10}$

Таким образом, квадратный трёхчлен будет принимать только отрицательные значения, если коэффициент $c$ — отрицательное число, модуль которого больше $\frac{3}{10}$.

Ответ: $c \in (-\infty; -\frac{3}{10})$

Пример: при $c = -1$ получаем трёхчлен $-x^2 — 3x — 25$, который всегда отрицателен при любом $x \in \mathbb{R}$.