Краткий ответ:
а) 15 − 2 a − a 2 + 1 2 a 2 − 2 \sqrt{15 — 2a — a^2} + \sqrt{\frac{1}{2}a^2 — 2}
Имеет смысл при:
{ 15 − 2 a − a 2 ≥ 0 1 2 a 2 − 2 ≥ 0 \begin{cases} 15 — 2a — a^2 \geq 0 \\ \frac{1}{2}a^2 — 2 \geq 0 \end{cases} 1) 15 − 2 a − a 2 ≥ 0 15 — 2a — a^2 \geq 0
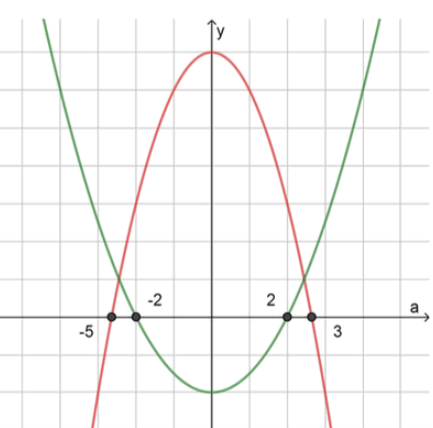
Ветви параболы направлены вниз;
Нули функции:
− a 2 − 2 a + 15 = 0 ; -a^2 — 2a + 15 = 0;
D = 2 2 + 4 ⋅ 15 = 4 + 60 = 64 = 8 2 , тогда: D = 2^2 + 4 \cdot 15 = 4 + 60 = 64 = 8^2, \text{ тогда:}
a 1 = 2 − 8 − 2 = 3 и a 2 = 2 + 8 − 2 = − 5 ; a_1 = \frac{2 — 8}{-2} = 3 \quad \text{и} \quad a_2 = \frac{2 + 8}{-2} = -5;
2) 1 2 a 2 − 2 ≥ 0 \frac{1}{2}a^2 — 2 \geq 0
Ветви параболы направлены вверх;
Нули функции:
1 2 a 2 − 2 = 0 ∣ ⋅ 2 ; \frac{1}{2}a^2 — 2 = 0 \quad | \cdot 2;
a 2 − 4 = 0 ; a^2 — 4 = 0;
a 2 = 4 , отсюда a = ± 2 ; a^2 = 4, \text{ отсюда } a = \pm 2;
Схематичный рисунок:
3 ) { − 5 ≤ a ≤ 3 ( − ∞ ; − 2 ] ∪ [ 2 ; + ∞ ) ; 3) \begin{cases} -5 \leq a \leq 3 \\ (-\infty; -2] \cup [2; +\infty) \end{cases};
Ответ: [ − 5 ; − 2 ] ∪ [ 2 ; 3 ] [-5; -2] \cup [2; 3]
б) 1 − 1 4 a + 33 + 5 a − 2 a 2 \sqrt{1 — \frac{1}{4}a} + \sqrt{33 + 5a — 2a^2}
Имеет смысл при:
{ 1 − 1 4 a ≥ 0 33 + 5 a − 2 a 2 ≥ 0 \begin{cases} 1 — \frac{1}{4}a \geq 0 \\ 33 + 5a — 2a^2 \geq 0 \end{cases}
1) 1 − 1 4 a ≥ 0 1 — \frac{1}{4}a \geq 0
− a ≥ − 4 ; -a \geq -4;
a ≤ 4 ; a \leq 4;
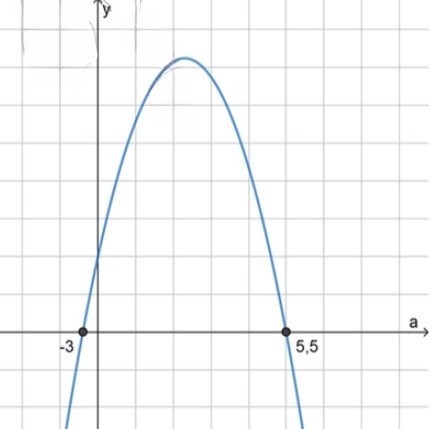
2 ) − 2 a 2 + 5 a + 33 ≥ 0 ;
Ветви параболы направлены вниз;
Нули функции:
− 2 a 2 + 5 a + 33 = 0 ; -2a^2 + 5a + 33 = 0;
D = 5 2 + 4 ⋅ 2 ⋅ 33 = 25 + 264 = 289 = 17 2 , тогда: D = 5^2 + 4 \cdot 2 \cdot 33 = 25 + 264 = 289 = 17^2, \text{ тогда:}
a 1 = − 5 − 17 2 ⋅ ( − 2 ) = 22 4 = 5.5 и a 2 = − 5 + 17 2 ⋅ ( − 2 ) = − 3 ; a_1 = \frac{-5 — 17}{2 \cdot (-2)} = \frac{22}{4} = 5.5 \quad \text{и} \quad a_2 = \frac{-5 + 17}{2 \cdot (-2)} = -3;
Схематический рисунок:
3 ) { a ≤ 4 − 3 ≤ a ≤ 5.5 ⟹ − 3 ≤ a ≤ 4 ; 3) \begin{cases} a \leq 4 \\ -3 \leq a \leq 5.5 \end{cases} \implies -3 \leq a \leq 4; [ − 3 ; 4 ] [-3; 4]
Подробный ответ:
а) 15 − 2 a − a 2 + 1 2 a 2 − 2 \sqrt{15 — 2a — a^2} + \sqrt{\frac{1}{2}a^2 — 2}
Выражение имеет смысл тогда и только тогда, когда подкоренные выражения неотрицательны. Запишем это условие:
15 − 2 a − a 2 ≥ 0 и 1 2 a 2 − 2 ≥ 0 15 — 2a — a^2 \geq 0 \quad \text{и} \quad \frac{1}{2}a^2 — 2 \geq 0
Рассмотрим сначала первое неравенство:
15 − 2 a − a 2 ≥ 0 15 — 2a — a^2 \geq 0
Приведём его к стандартному виду квадратного неравенства. Для этого перепишем в виде:
− a 2 − 2 a + 15 ≥ 0 -a^2 — 2a + 15 \geq 0
Домножим обе части на − 1 -1
a 2 + 2 a − 15 ≤ 0 a^2 + 2a — 15 \leq 0
Решим соответствующее уравнение:
a 2 + 2 a − 15 = 0 a^2 + 2a — 15 = 0
Найдём дискриминант:
D = 2 2 − 4 ⋅ 1 ⋅ ( − 15 ) = 4 + 60 = 64 D = 2^2 — 4 \cdot 1 \cdot (-15) = 4 + 60 = 64
Корни уравнения:
a 1 = − 2 − 8 2 = − 5 a_1 = \frac{-2 — 8}{2} = -5 a 2 = − 2 + 8 2 = 3 a_2 = \frac{-2 + 8}{2} = 3
Так как ветви параболы вверх, знак неравенства≤ 0 \leq 0
− 5 ≤ a ≤ 3 -5 \leq a \leq 3
Теперь второе неравенство:
1 2 a 2 − 2 ≥ 0 \frac{1}{2}a^2 — 2 \geq 0
Умножим обе части на 2:
a 2 − 4 ≥ 0 a^2 — 4 \geq 0
Найдём корни уравнения:
a 2 = 4 ⇒ a = ± 2 a^2 = 4 \Rightarrow a = \pm 2
Это неравенство имеет вид
a 2 − 4 ≥ 0 a^2 — 4 \geq 0 ≥ \geq
a ≤ − 2 или a ≥ 2 a \leq -2 \quad \text{или} \quad a \geq 2
Пересечём оба множества:
Первое: − 5 ≤ a ≤ 3 -5 \leq a \leq 3
Второе: a ≤ − 2 или a ≥ 2 a \leq -2 \quad \text{или} \quad a \geq 2
Тогда пересечение: [ − 5 ; − 2 ] ∪ [ 2 ; 3 ] [-5; -2] \cup [2; 3]
Ответ: [ − 5 ; − 2 ] ∪ [ 2 ; 3 ] [-5; -2] \cup [2; 3]
б) 1 − 1 4 a + 33 + 5 a − 2 a 2 \sqrt{1 — \frac{1}{4}a} + \sqrt{33 + 5a — 2a^2}
Найти область определения — значит решить систему двух неравенств:
1 − 1 4 a ≥ 0 и 33 + 5 a − 2 a 2 ≥ 0 1 — \frac{1}{4}a \geq 0 \quad \text{и} \quad 33 + 5a — 2a^2 \geq 0
Сначала первое неравенство:
1 − 1 4 a ≥ 0 1 — \frac{1}{4}a \geq 0
Переносим и домножим:
− 1 4 a ≥ − 1 ⇒ a ≤ 4 -\frac{1}{4}a \geq -1 \Rightarrow a \leq 4
Теперь второе неравенство:
− 2 a 2 + 5 a + 33 ≥ 0 ;
Перепишем в стандартном виде:
− 2 a 2 + 5 a + 33 ≥ 0 -2a^2 + 5a + 33 \geq 0
Решим уравнение:
− 2 a 2 + 5 a + 33 = 0 -2a^2 + 5a + 33 = 0
Дискриминант:
D = 5 2 − 4 ⋅ ( − 2 ) ⋅ 33 = 25 + 264 = 289 D = 5^2 — 4 \cdot (-2) \cdot 33 = 25 + 264 = 289
Корни:
a 1 = − 5 − 17 − 4 = 22 4 = 5.5 a_1 = \frac{-5 — 17}{-4} = \frac{22}{4} = 5.5 a 2 = − 5 + 17 − 4 = − 12 − 4 = 3 a_2 = \frac{-5 + 17}{-4} = \frac{-12}{-4} = 3
Так как ветви параболы направлены вниз, знак≥ \geq
3 ≤ a ≤ 5.5 3 \leq a \leq 5.5
Теперь найдём пересечение с условием a ≤ 4 a \leq 4
Пересекаются промежутки: a ≤ 4 a \leq 4 3 ≤ a ≤ 5.5 3 \leq a \leq 5.5
Ответ: 3 ≤ a ≤ 4 3 \leq a \leq 4
Ответ: [ 3 ; 4 ] [3; 4]





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!