ГДЗ по Алгебре 9 Класс Номер 335 Дорофеев, Суворова — Подробные Ответы

Найдите целые решения неравенства:

а) $\frac{2x^2}{3} < \frac{2x + 3}{4}$;

б) $\frac{4x + 2}{3} > \frac{5x^2}{6}$;

в) $(x + 2\sqrt{3})(x + 3\sqrt{2}) < 0$;

г) $(x + 1 — \sqrt{5})(x + 1 — \sqrt{6}) \leq 0$.

а) $\frac{2x^2}{3} < \frac{2x + 3}{4}$:

Умножим обе части на 12:
$4 \cdot 2x^2 < 3(2x + 3);$
$8x^2 < 6x + 9;$
$8x^2 — 6x — 9 < 0;$

$a = 8 > 0$, значит ветви направлены вверх;

2) Нули функции:
$8x^2 — 6x — 9 = 0;$
$D = 6^2 + 4 \cdot 8 \cdot 9 = 36 + 288 = 324 = 18^2, \text{ тогда:}$
$x_1 = \frac{6 — 18}{2 \cdot 8} = -\frac{3}{4}$
$x_2=\frac{6+18}{2\cdot 8}=\frac{24}{16}=1\frac{1}{2}$

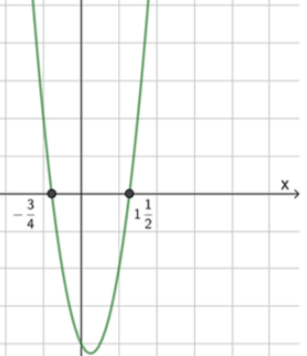
3) Схематический рисунок

$$-\frac{3}{4} < x < 1\frac{1}{2};$$
Целые решения: $0; 1$

б) $\frac{4x + 2}{3} > \frac{5x^2}{6}$:

Умножим обе части на 6:
$2(4x + 2) > 5x^2;$
$8x + 4 > 5x^2;$
$-5x^2 + 8x + 4 > 0;$

$a = -5 < 0$, значит ветви направлены вниз;

2) Нули функции:
$-5x^2 + 8x + 4 = 0;$
$D = 8^2 + 4 \cdot 5 \cdot 4 = 64 + 80 = 144, \text{ тогда:}$
$x_1 = \frac{-8 — 12}{2 \cdot (-5)} = 2$
$x_2=\frac{-8+12}{2\cdot (-5)}=-\mathrm{0,4}$

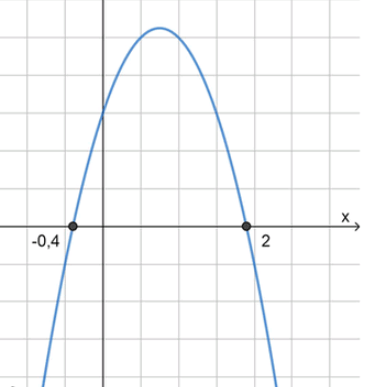
3) Схематический рисунок$3) Схематический рисунок3) Схематический рисунок$

$3) Схематический рисунокx_2 = \frac{-8 + 12}{2 \cdot (-5)} = -0{,}4$

-0,4 < х < 2;

Целые решения: $0; 1$

в) $(x + 2\sqrt{3})(x + 3\sqrt{2}) < 0$:

$a = 1 > 0$, значит ветви направлены вверх;

2) Нули функции:
$x_1 + 2\sqrt{3} = 0 \Rightarrow x_1 = -2\sqrt{3} \approx -3{,}46$
$x_2+3\sqrt{2}=0\Rightarrow x_2=-3\sqrt{2}\approx -\mathrm{4,24}$

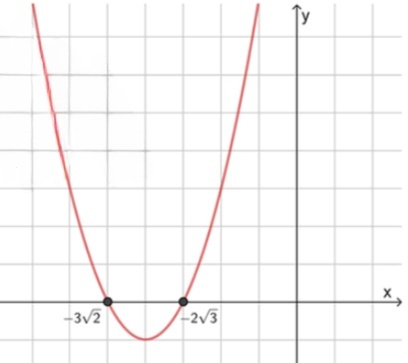
3) Схематический рисунок

$3) Схематический рисунокx_2 + 3\sqrt{2} = 0 \Rightarrow x_2 = -3\sqrt{2} \approx -4{,}24$

$$-3\sqrt{2} < x < -2\sqrt{3};$$
Целое решение: $-4$

г) $(x + 1 — \sqrt{5})(x + 1 — \sqrt{6}) \leq 0$:

$a = 1 > 0$, значит ветви направлены вверх;

2) Нули функции:
$x_1 + 1 — \sqrt{5} = 0 \Rightarrow x_1 = \sqrt{5} — 1 \approx 1{,}23$
$x_2+1-\sqrt{6}=0\Rightarrow x_2=\sqrt{6}-1\approx \mathrm{1,45}$

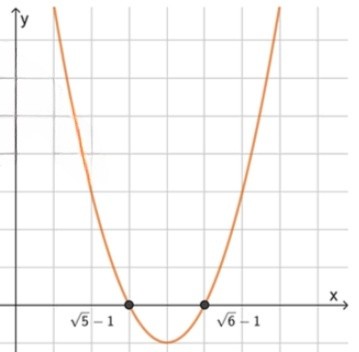
3) Схематический рисунок

$$\sqrt{5} — 1 < x < \sqrt{6} — 1;$$

Целые решения отсутствуют.

а) $\frac{2x^2}{3} < \frac{2x + 3}{4}$

умножим обе части неравенства на 12 (наименьшее общее кратное знаменателей 3 и 4), чтобы избавиться от дробей:

$12 \cdot \frac{2x^2}{3} < 12 \cdot \frac{2x + 3}{4}$

$4 \cdot 2x^2 < 3(2x + 3)$

$8x^2 < 6x + 9$

переносим все слагаемые в левую часть и приводим подобные:

$8x^2 — 6x — 9 < 0$

это квадратное неравенство с коэффициентами:

$a = 8,\ b = -6,\ c = -9$

так как $a > 0$, ветви параболы направлены вверх, значит выражение меньше нуля между корнями

находим дискриминант:

$D = (-6)^2 — 4 \cdot 8 \cdot (-9) = 36 + 288 = 324$

так как $D > 0$, уравнение имеет два различных вещественных корня

находим корни по формуле:

$x_1 = \frac{-(-6) — \sqrt{324}}{2 \cdot 8} = \frac{6 — 18}{16} = -\frac{12}{16} = -\frac{3}{4}$

$x_2 = \frac{-(-6) + \sqrt{324}}{2 \cdot 8} = \frac{6 + 18}{16} = \frac{24}{16} = \frac{3}{2}$

так как неравенство строгое и парабола вверх, решением будет промежуток между корнями:

$x \in \left(-\frac{3}{4}; \frac{3}{2}\right)$

целые числа, принадлежащие этому промежутку: 0 и 1

ответ: $0;1$

б) $\frac{4x + 2}{3} > \frac{5x^2}{6}$

умножаем обе части на 6:

$6 \cdot \frac{4x + 2}{3} > 6 \cdot \frac{5x^2}{6}$

$2(4x + 2) > 5x^2$

$8x + 4 > 5x^2$

переносим все влево:

$-5x^2 + 8x + 4 > 0$

или

$5x^2 — 8x — 4 < 0$

умножим на (-1), при этом меняется знак неравенства

коэффициенты:

$a = -5,\ b = 8,\ c = 4$

ветви параболы направлены вниз, так как $a < 0$, значит выражение больше нуля между корнями

находим дискриминант:

$D = 8^2 — 4 \cdot (-5) \cdot 4 = 64 + 80 = 144$

корни:

$x_1 = \frac{-8 — \sqrt{144}}{2 \cdot (-5)} = \frac{-8 — 12}{-10} = \frac{-20}{-10} = 2$

$x_2 = \frac{-8 + \sqrt{144}}{2 \cdot (-5)} = \frac{-8 + 12}{-10} = \frac{4}{-10} = -\frac{2}{5}$

решение неравенства:

$x \in \left(-\frac{2}{5}; 2\right)$

целые числа из этого промежутка: 0 и 1

ответ: $0;1$

в) $(x + 2\sqrt{3})(x + 3\sqrt{2}) < 0$

здесь произведение двух линейных множителей, значит корни:

$x_1 = -2\sqrt{3} \approx -3.464$

$x_2 = -3\sqrt{2} \approx -4.243$

поскольку $-4.243 < -3.464$, то меньшее из двух — $x_2$, большее — $x_1$

так как коэффициент при $x^2$ положительный, ветви параболы направлены вверх, и выражение будет меньше нуля между корнями:

$x \in (-3\sqrt{2}; -2\sqrt{3})$

приблизительно: $x \in (-4.243; -3.464)$

единственное целое число в этом промежутке — $-4$

ответ: $-4$

г) $(x + 1 — \sqrt{5})(x + 1 — \sqrt{6}) \leq 0$

корни:

$x_1 = \sqrt{5} — 1 \approx 2.236 — 1 = 1.236$

$x_2 = \sqrt{6} — 1 \approx 2.449 — 1 = 1.449$

меньший корень: $x_1$, больший — $x_2$

ветви параболы направлены вверх, значит неравенство выполняется на отрезке между корнями включительно:

$x \in [\sqrt{5} — 1;\ \sqrt{6} — 1] \approx [1.236;\ 1.449]$

в этом отрезке нет целых чисел

ответ: нет решений