Краткий ответ:
а) y = { 6 x , если x > 2 ; x 2 − 1 , если ∣ x ∣ ≤ 2 ; − 6 x , если x < − 2 ; y = \begin{cases} \frac{6}{x}, & \text{если } x > 2; \\ x^2 — 1, & \text{если } |x| \leq 2; \\ -\frac{6}{x}, & \text{если } x < -2; \end{cases}
1) y = 6 x y = \frac{6}{x}
x 2 3 6 y 3 2 1 \begin{array}{|c|c|c|c|} \hline x & 2 & 3 & 6 \\ \hline y & 3 & 2 & 1 \\ \hline \end{array}
2) x 2 − 1 x^2 — 1
x 0 = 0 x_0 = 0 y 0 = − 1 y_0 = -1
x − 2 − 1 1 2 y 3 0 0 3 \begin{array}{|c|c|c|c|c|} \hline x & -2 & -1 & 1 & 2 \\ \hline y & 3 & 0 & 0 & 3 \\ \hline \end{array}
3) y = − 6 x y = -\frac{6}{x}
x − 6 − 3 − 2 y 1 2 3 \begin{array}{|c|c|c|c|} \hline x & -6 & -3 & -2 \\ \hline y & 1 & 2 & 3 \\ \hline \end{array}
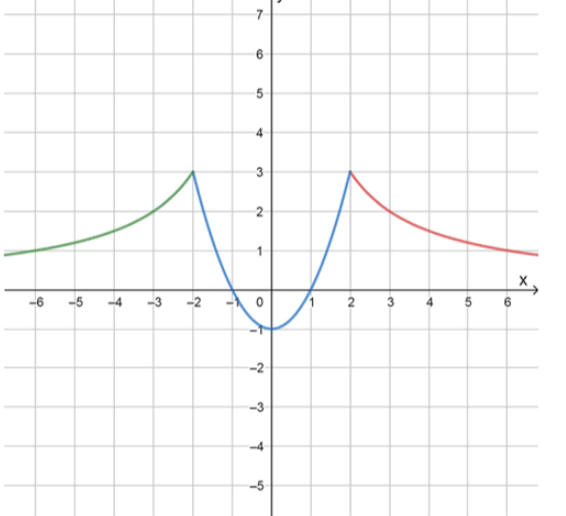
График искомой функции:
Положительные значения при: x ∈ ( − ∞ ; − 1 ) ∪ ( 1 ; + ∞ ) x \in (-\infty; -1) \cup (1; +\infty)
Отрицательные значения при: x ∈ ( − 1 ; 1 ) x \in (-1; 1)
б) y = { 4 − 2 x , если x > 1 ; x 2 + 1 , если ∣ x ∣ ≤ 1 ; 4 + 2 x , если x < − 1 ; y = \begin{cases} 4 — 2x, & \text{если } x > 1; \\ x^2 + 1, & \text{если } |x| \leq 1; \\ 4 + 2x, & \text{если } x < -1; \end{cases}
1) y = 4 − 2 x y = 4 — 2x
x 1 2 y 2 0 \begin{array}{|c|c|c|} \hline x & 1 & 2 \\ \hline y & 2 & 0 \\ \hline \end{array}
2) x 2 + 1 x^2 + 1
x 0 = 0 x_0 = 0 y 0 = 1 y_0 = 1
x − 1 1 y 2 2 \begin{array}{|c|c|c|} \hline x & -1 & 1 \\ \hline y & 2 & 2 \\ \hline \end{array}
3) y = 4 + 2 x y = 4 + 2x
x − 2 − 1 y 0 2 \begin{array}{|c|c|c|} \hline x & -2 & -1 \\ \hline y & 0 & 2 \\ \hline \end{array}
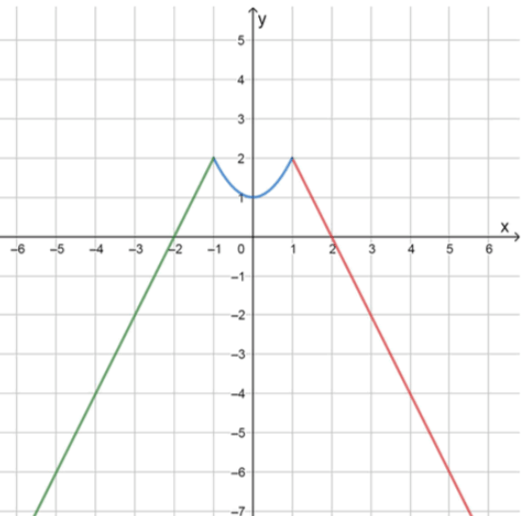
График искомой функции:
Положительные значения при: x ∈ ( − 2 ; 2 ) x \in (-2; 2)
Отрицательные значения при: x ∈ ( − ∞ ; − 2 ) ∪ ( 2 ; + ∞ ) x \in (-\infty; -2) \cup (2; +\infty)
Подробный ответ:
а) y = { 6 x , если x > 2 ; x 2 − 1 , если ∣ x ∣ ≤ 2 ; − 6 x , если x < − 2 ; y = \begin{cases} \frac{6}{x}, & \text{если } x > 2; \\ x^2 — 1, & \text{если } |x| \leq 2; \\ -\frac{6}{x}, & \text{если } x < -2; \end{cases}
Рассмотрим каждый участок функции по отдельности.
Первый участок: y = 6 x y = \frac{6}{x} x > 2 x > 2
Это гипербола с разрывом в точке x = 0 x = 0 x > 2 x > 2 x x
При x = 2 x = 2 y = 6 2 = 3 y = \frac{6}{2} = 3
При x = 3 x = 3 y = 6 3 = 2 y = \frac{6}{3} = 2
При x = 6 x = 6 y = 6 6 = 1 y = \frac{6}{6} = 1
Запишем значения в таблицу:
x 2 3 6 y 3 2 1 \begin{array}{|c|c|c|c|} \hline x & 2 & 3 & 6 \\ \hline y & 3 & 2 & 1 \\ \hline \end{array}
Второй участок: y = x 2 − 1 y = x^2 — 1 ∣ x ∣ ≤ 2 |x| \leq 2 − 2 ≤ x ≤ 2 -2 \leq x \leq 2
Это уравнение параболы с вершиной в точке ( 0 , − 1 ) (0, -1) x 0 = 0 x_0 = 0 y 0 = − 1 y_0 = -1
При x = − 2 x = -2 y = ( − 2 ) 2 − 1 = 4 − 1 = 3 y = (-2)^2 — 1 = 4 — 1 = 3
При x = − 1 x = -1 y = ( − 1 ) 2 − 1 = 1 − 1 = 0 y = (-1)^2 — 1 = 1 — 1 = 0
При x = 1 x = 1 y = 1 2 − 1 = 1 − 1 = 0 y = 1^2 — 1 = 1 — 1 = 0
При x = 2 x = 2 y = 4 − 1 = 3 y = 4 — 1 = 3
Таблица:
x − 2 − 1 1 2 y 3 0 0 3 \begin{array}{|c|c|c|c|c|} \hline x & -2 & -1 & 1 & 2 \\ \hline y & 3 & 0 & 0 & 3 \\ \hline \end{array}
Третий участок: y = − 6 x y = -\frac{6}{x} x < − 2 x < -2
Это тоже гипербола, но с противоположным знаком.
При x = − 6 x = -6 y = − 6 − 6 = 1 y = -\frac{6}{-6} = 1
При x = − 3 x = -3 y = − 6 − 3 = 2 y = -\frac{6}{-3} = 2
При x = − 2 x = -2 y = − 6 − 2 = 3 y = -\frac{6}{-2} = 3
Таблица:
x − 6 − 3 − 2 y 1 2 3 \begin{array}{|c|c|c|c|} \hline x & -6 & -3 & -2 \\ \hline y & 1 & 2 & 3 \\ \hline \end{array}
Промежутки знакопостоянства функции:
Положительные значения функция принимает на тех промежутках, где значения y > 0 y > 0
При x < − 1 x < -1 y = − 6 x y = -\frac{6}{x} − 6 -6
При x > 1 x > 1 y = 6 x y = \frac{6}{x} x > 0 x > 0
Значит:
Положительные значения при x ∈ ( − ∞ ; − 1 ) ∪ ( 1 ; + ∞ ) x \in (-\infty; -1) \cup (1; +\infty)
Отрицательные значения при x ∈ ( − 1 ; 1 ) x \in (-1; 1) x 2 − 1 < 0 x^2 — 1 < 0
б) y = { 4 − 2 x , если x > 1 ; x 2 + 1 , если ∣ x ∣ ≤ 1 ; 4 + 2 x , если x < − 1 ; y = \begin{cases} 4 — 2x, & \text{если } x > 1; \\ x^2 + 1, & \text{если } |x| \leq 1; \\ 4 + 2x, & \text{если } x < -1; \end{cases}
Рассмотрим все три части функции.
Первый участок: y = 4 − 2 x y = 4 — 2x x > 1 x > 1
Это линейная функция с угловым коэффициентом − 2 -2 x = 1 x = 1 y = 4 − 2 ⋅ 1 = 2 y = 4 — 2 \cdot 1 = 2
При x = 2 x = 2 y = 4 − 2 ⋅ 2 = 0 y = 4 — 2 \cdot 2 = 0
Таблица:
x 1 2 y 2 0 \begin{array}{|c|c|c|} \hline x & 1 & 2 \\ \hline y & 2 & 0 \\ \hline \end{array}
Второй участок: y = x 2 + 1 y = x^2 + 1 − 1 ≤ x ≤ 1 -1 \leq x \leq 1
Это парабола, которая принимает наименьшее значение при x = 0 x = 0 y = 0 2 + 1 = 1 y = 0^2 + 1 = 1
При x = − 1 x = -1 y = 1 + 1 = 2 y = 1 + 1 = 2 x = 1 x = 1 y = 1 + 1 = 2 y = 1 + 1 = 2
Таблица:
x − 1 1 y 2 2 \begin{array}{|c|c|c|} \hline x & -1 & 1 \\ \hline y & 2 & 2 \\ \hline \end{array}
Третий участок: y = 4 + 2 x y = 4 + 2x x < − 1 x < -1
Это линейная функция с угловым коэффициентом + 2 +2
При x = − 2 x = -2 y = 4 + 2 ⋅ ( − 2 ) = 0 y = 4 + 2 \cdot (-2) = 0 x = − 1 x = -1 y = 4 + 2 ⋅ ( − 1 ) = 2 y = 4 + 2 \cdot (-1) = 2
Таблица:
x − 2 − 1 y 0 2 \begin{array}{|c|c|c|} \hline x & -2 & -1 \\ \hline y & 0 & 2 \\ \hline \end{array}
Анализируем знаки значений:
Положительные значения:x 2 + 1 > 0 x^2 + 1 > 0 4 + 2 x > 0 4 + 2x > 0 x > − 2 x > -2 4 − 2 x > 0 4 — 2x > 0 x < 2 x < 2
Значит:
Положительные значения при x ∈ ( − 2 ; 2 ) x \in (-2; 2)
Отрицательные значения при x ∈ ( − ∞ ; − 2 ) ∪ ( 2 ; + ∞ ) x \in (-\infty; -2) \cup (2; +\infty)





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!