
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 329 Дорофеев, Суворова — Подробные Ответы
Постройте график функции:
а) . По графику определите, какие значения принимает функция, если .
б) . По графику определите, какие значения принимает функция, если .
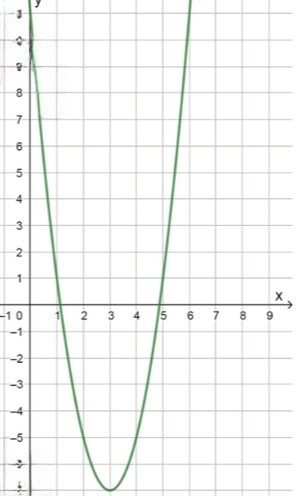
а) :
, значит ветви направлены вверх;
2) Координаты вершины параболы:
3) Координаты некоторых точек:
График искомой функции:
При принимает значения: .
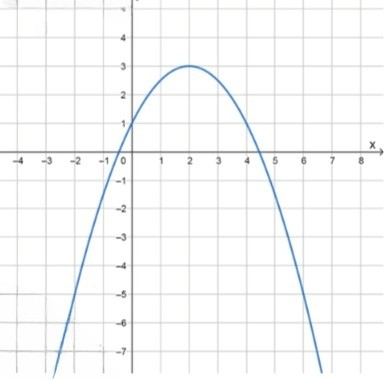
б) :
, значит ветви направлены вниз;
2) Координаты вершины параболы:
3) Координаты некоторых точек:
График искомой функции:
При принимает значения: .
а)
коэффициент при : , значит ветви параболы направлены вверх
приведём квадратный трёхчлен к вершиной форме:
используем формулу координаты вершины:
найдём значение функции в точке вершины:
вершина параболы:
подставим значения для построения таблицы:
при :
при :
при :
при :
при :
при :
таблица значений:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| 11 | 1 | -5 | -7 | -5 | 1 | 11 |
минимальное значение достигается в вершине, при :
максимальное значение на отрезке — при :
при , значения функции
б)
коэффициент при : , значит ветви параболы направлены вниз
найдём координаты вершины:
значение функции в вершине:
вершина параболы:
подставим значения для построения таблицы:
при :
при :
при :
при :
таблица значений:
| -2 | 0 | 2 | 4 | 6 | |
|---|---|---|---|---|---|
| -5 | 1 | 3 | 1 | -5 |
максимум функции при :
минимальное значение на отрезке :
при , значения функции




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!