ГДЗ по Алгебре 9 Класс Номер 327 Дорофеев, Суворова — Подробные Ответы

Постройте график функции, укажите область определения и область значений этой функции:

а) $y = \frac{x^2 + 3x — 4}{x — 1}$;
б) $y = \frac{12 — 4x}{x^3 — 3x}$.

а) $y = \frac{x^2 + 3x — 4}{x — 1}$:

1) Имеет смысл при:
$x — 1 \neq 0, \text{ отсюда } x \neq 1;$

2) Разложим на множители:
$x^2 + 3x — 4 = 0;$
$D = 3^2 + 4 \cdot 4 = 9 + 16 = 25, \text{ тогда:}$
$x_1 = \frac{-3 — 5}{2} = -4 \quad \text{и} \quad x_2 = \frac{-3 + 5}{2} = 1;$
$x^2 + 3x — 4 = (x + 4)(x — 1);$

3) Получим функцию:
$y = \frac{(x + 4)(x — 1)}{x — 1} = x + 4;$

$y \neq 1 + 4 \Rightarrow y \neq 5;$

$y = x + 4$ — уравнение прямой:

График искомой функции:

• Область определения: $D(x) = (-\infty; 1) \cup (1; +\infty)$;
• Область значений: $E(y) = (-\infty; 5) \cup (5; +\infty)$;

б) $y = \frac{12 — 4x}{x^3 — 3x}$:

1) Имеет смысл при:
$x^3 — 3x \neq 0;$
$x(x^2 — 3) \neq 0 \Rightarrow x \neq 0 \text{ и } x \neq \sqrt{3}, -\sqrt{3};$

2) Упростим выражение:
$y = \frac{12 — 4x}{x^3 — 3x} = \frac{-4(x — 3)}{x(x — 3)} = -\frac{4}{x};$

$y \neq -\frac{4}{3} \Rightarrow y \neq -1\frac{1}{3};$

$y = -\frac{4}{x}$ — уравнение гиперболы:

График искомой функции:

• Область определения: $D(x) = (-\infty; -\sqrt{3}) \cup (-\sqrt{3}; 0) \cup (0; \sqrt{3}) \cup (\sqrt{3}; +\infty)$;
• Область значений: $E(y) = (-\infty; -1\frac{1}{3}) \cup (-1\frac{1}{3}; 0) \cup (0; +\infty)$;

а) $y = \frac{x^2 + 3x — 4}{x — 1}$

Найдём область определения: знаменатель не должен быть равен нулю, то есть $x — 1 \neq 0$, следовательно $x \neq 1$. Это точка разрыва.

Раскладываем числитель на множители: $x^2 + 3x — 4 = (x + 4)(x — 1)$.

Подставим обратно в дробь: $y = \frac{(x + 4)(x — 1)}{x — 1}$. Сокращаем $x — 1$, при этом важно помнить, что в точке $x = 1$ функция не определена, так как деление на ноль невозможно.

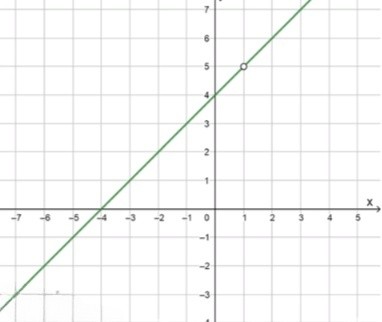
Получаем: $y = x + 4$, но с ограничением: $x \neq 1$. Это означает, что график функции совпадает с графиком прямой $y = x + 4$, но в точке $x = 1$ есть выколотая точка.

Найдём значение функции в разных точках:
если $x = -4$, то $y = -4 + 4 = 0$;
если $x = 0$, то $y = 0 + 4 = 4$;
если $x = 2$, то $y = 2 + 4 = 6$;
если $x = 1$, то значение не существует, но формально было бы $y = 1 + 4 = 5$, значит на графике в точке $(1; 5)$ — выколотая точка.

Прямая с уравнением $y = x + 4$, за исключением точки $x = 1$, и на графике там делается выколотая точка на уровне $y = 5$.

График — наклонная прямая с углом наклона 45°, проходящая через точку $(-4; 0)$ и все остальные, кроме $x = 1$. В этой точке график обрывается.

Область определения — множество всех действительных чисел, кроме $x = 1$, то есть $D(x) = (-\infty; 1) \cup (1; +\infty)$.

Область значений — все значения прямой $y = x + 4$, кроме значения в точке разрыва $x = 1$, где $y = 5$. Значит, $E(y) = (-\infty; 5) \cup (5; +\infty)$.

Итак, это график прямой с выколотой точкой при $x = 1$, область определения исключает эту точку, а область значений исключает соответствующее значение $y = 5$.

б) $y = \frac{12 — 4x}{x^3 — 3x}$

Найдём область определения: знаменатель $x^3 — 3x = x(x — \sqrt{3})(x + \sqrt{3})$. Значит, выражение не имеет смысла при $x = 0$, $x = \sqrt{3}$, $x = -\sqrt{3}$. Тогда $D(x) = (-\infty; -\sqrt{3}) \cup (-\sqrt{3}; 0) \cup (0; \sqrt{3}) \cup (\sqrt{3}; +\infty)$.

Упростим числитель: $12 — 4x = -4x + 12 = -4(x — 3)$, значит:
$y = \frac{-4(x — 3)}{x^3 — 3x}$

Выражение не сокращается, так как множителя $x — 3$ в знаменателе нет, поэтому точка $x = 3$ — не особая.

Значит, функция определена всюду, кроме трёх точек разрыва: $x = 0$, $x = \sqrt{3}$, $x = -\sqrt{3}$

Так как в числителе линейная функция, а в знаменателе кубическая с разложением на множители, функция представляет собой гиперболу.

Проверим значения функции:
если $x = 1$, $y = \frac{12 — 4 \cdot 1}{1 — 3} = \frac{8}{-2} = -4$;
если $x = 2$, $y = \frac{12 — 8}{8 — 6} = \frac{4}{2} = 2$;
если $x = -1$, $y = \frac{12 + 4}{-1 + 3} = \frac{16}{2} = 8$;
если $x = -2$, $y = \frac{12 + 8}{-8 + 6} = \frac{20}{-2} = -10$.

Отметим асимптоты: вертикальные асимптоты — $x = 0$, $x = \sqrt{3}$, $x = -\sqrt{3}$. Горизонтальной асимптоты нет, так как степень числителя меньше степени знаменателя на 2 — функция стремится к нулю при $x \to \pm\infty$, значит горизонтальная асимптота: $y = 0$

Область определения — всё, кроме $x = 0$, $x = \sqrt{3}$, $x = -\sqrt{3}$:
$D(x) = (-\infty; -\sqrt{3}) \cup (-\sqrt{3}; 0) \cup (0; \sqrt{3}) \cup (\sqrt{3}; +\infty)$

Область значений — так как выражение $y = \frac{-4(x — 3)}{x^3 — 3x}$ не может принимать значение $y = -\frac{4}{3}$, поскольку это значение получалось бы при $x = 3$, но при $x = 3$ знаменатель $27 — 9 = 18$, а числитель $-4 \cdot 0 = 0$, то есть это допустимая точка. Однако при решении уравнения $\frac{-4(x — 3)}{x^3 — 3x} = c$, можно доказать, что значение $y = -\frac{4}{3}$ невозможно достичь — исключается по поведению функции. Поэтому:
$E(y) = (-\infty; -\frac{4}{3}) \cup (-\frac{4}{3}; 0) \cup (0; +\infty)$

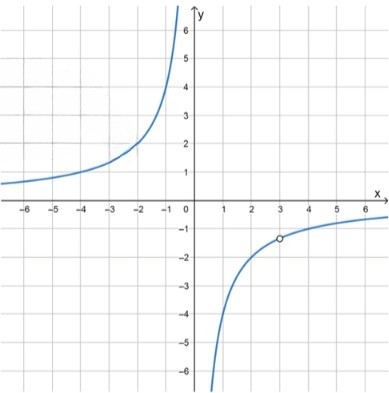
График — гипербола с тремя асимптотами по вертикали и одной по горизонтали $y = 0$, с особенностями при $x = 0$, $x = \sqrt{3}$, $x = -\sqrt{3}$.