ГДЗ по Алгебре 9 Класс Номер 326 Дорофеев, Суворова — Подробные Ответы

Постройте график уравнения:

а) $|y| = |x|$;
б) $|y| \cdot |x| = 1$;
в) $|y| + |x| = 1$;
г) $|y| — |x| = 1$.

Указание. Рассмотрите уравнение отдельно для каждой координатной четверти.

а) $|y| = |x|$:

1 координатная четверть:
$y > 0$, $x > 0$ → $|y| = |x|$ ⇔ $y = x$

2 координатная четверть:
$y > 0$, $x < 0$ → $|y| = |x|$ ⇔ $y = -x$

3 координатная четверть:
$y < 0$, $x < 0$ → $|y| = |x|$ ⇔ $-y = -x$ ⇔ $y = x$

4 координатная четверть:
$y < 0$, $x > 0$ → $|y| = |x|$ ⇔ $-y = x$ ⇔ $y = -x$

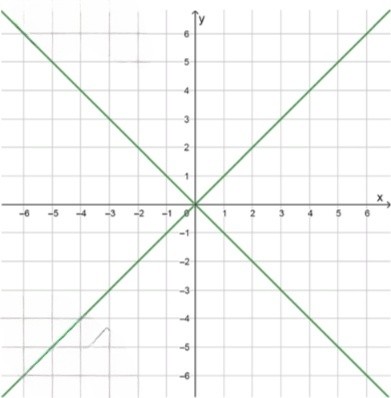
График искомой функции:

б) $|y| \cdot |x| = 1$:

1 координатная четверть:
$y > 0$, $x > 0$ → $|y| \cdot |x| = yx = 1$ ⇔ $y = \frac{1}{x}$

2 координатная четверть:
$y > 0$, $x < 0$ → $|y| \cdot |x| = y(-x) = 1$ ⇔ $y = -\frac{1}{x}$

3 координатная четверть:
$y < 0$, $x < 0$ → $|y| \cdot |x| = (-y)(-x) = 1$ ⇔ $y = \frac{1}{x}$

4 координатная четверть:
$y < 0$, $x > 0$ → $|y| \cdot |x| = (-y)(x) = 1$ ⇔ $y = -\frac{1}{x}$

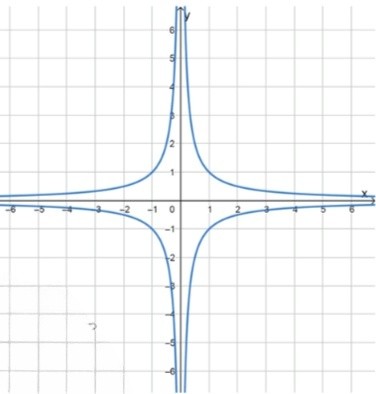
График искомой функции:

в) $|y| + |x| = 1$:

1 координатная четверть:
$y > 0$, $x > 0$ → $y + x = 1$ ⇔ $y = 1 — x$

2 координатная четверть:
$y > 0$, $x < 0$ → $y — x = 1$ ⇔ $y = 1 + x$

3 координатная четверть:
$y < 0$, $x < 0$ → $-y — x = 1$ ⇔ $y = -1 — x$

4 координатная четверть:
$y < 0$, $x > 0$ → $-y + x = 1$ ⇔ $y = x — 1$

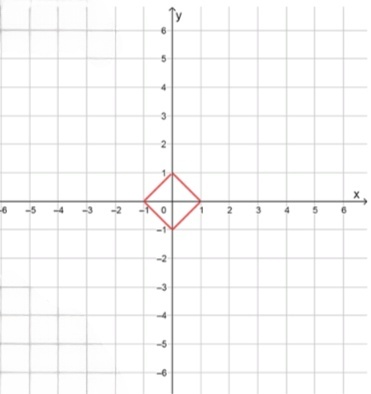
График искомой функции:

г) $|y| — |x| = 1$:

1 координатная четверть:
$y > 0$, $x > 0$ → $y — x = 1$ ⇔ $y = x + 1$

2 координатная четверть:
$y > 0$, $x < 0$ → $y + x = 1$ ⇔ $y = 1 — x$

3 координатная четверть:
$y < 0$, $x < 0$ → $-y + x = 1$ ⇔ $y = x — 1$

4 координатная четверть:
$y < 0$, $x > 0$ → $-y — x = 1$ ⇔ $y = -1 — x$

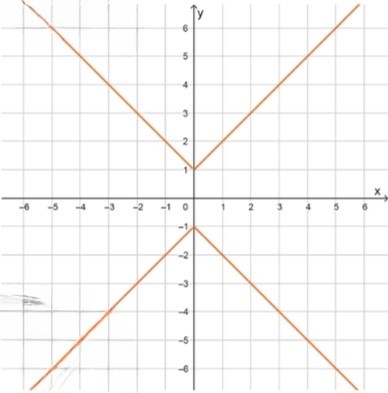
График искомой функции:

а) $|y| = |x|$

рассматриваем по четвертям:

1-я четверть: $x > 0$, $y > 0$
в этом случае модули раскрываются без изменения: $|y| = |x| \Rightarrow y = x$

2-я четверть: $x < 0$, $y > 0$
$|x| = -x$, $|y| = y$, тогда $y = -x$

3-я четверть: $x < 0$, $y < 0$
$|x| = -x$, $|y| = -y$, уравнение: $-y = -x \Rightarrow y = x$

4-я четверть: $x > 0$, $y < 0$
$|x| = x$, $|y| = -y$, уравнение: $-y = x \Rightarrow y = -x$

итог: график состоит из четырёх лучей: $y = x$, $y = -x$, симметричных относительно осей

точки:
$(-2, -2)$, $(-2, 2)$, $(2, -2)$, $(2, 2)$, $(0, 0)$

б) $|y| \cdot |x| = 1$

перепишем: $|x||y| = 1$

рассматриваем по четвертям:

1-я четверть: $x > 0$, $y > 0$
модули раскрываются как есть: $xy = 1 \Rightarrow y = \frac{1}{x}$

2-я четверть: $x < 0$, $y > 0$
$|x| = -x$, $|y| = y$: $(-x)y = 1 \Rightarrow y = -\frac{1}{x}$

3-я четверть: $x < 0$, $y < 0$
$|x| = -x$, $|y| = -y$: $(-x)(-y) = 1 \Rightarrow y = \frac{1}{x}$

4-я четверть: $x > 0$, $y < 0$
$|x| = x$, $|y| = -y$: $x(-y) = 1 \Rightarrow y = -\frac{1}{x}$

итог: гипербола, состоящая из четырёх ветвей:
$y = \frac{1}{x}$ в 1-й и 3-й четвертях,
$y = -\frac{1}{x}$ во 2-й и 4-й четвертях

точки:
$(1, 1)$, $(-1, 1)$, $(-1, -1)$, $(1, -1)$

в) $|y| + |x| = 1$

решим по четвертям:

1-я четверть: $x > 0$, $y > 0$: $x + y = 1 \Rightarrow y = 1 — x$

2-я четверть: $x < 0$, $y > 0$: $-x + y = 1 \Rightarrow y = 1 + x$

3-я четверть: $x < 0$, $y < 0$: $-x — y = 1 \Rightarrow y = -1 — x$

4-я четверть: $x > 0$, $y < 0$: $x — y = 1 \Rightarrow y = x — 1$

пересечения со сторонами ромба:
$(1, 0)$, $(0, 1)$, $(-1, 0)$, $(0, -1)$

фигура — ромб с вершинами на координатных осях

г) $|y| — |x| = 1$

анализ по четвертям:

1-я четверть: $x > 0$, $y > 0$: $y — x = 1 \Rightarrow y = x + 1$

2-я четверть: $x < 0$, $y > 0$: $y + x = 1 \Rightarrow y = 1 — x$

3-я четверть: $x < 0$, $y < 0$: $-y + x = 1 \Rightarrow y = x — 1$

4-я четверть: $x > 0$, $y < 0$: $-y — x = 1 \Rightarrow y = -1 — x$

получаются четыре луча, направленных из области вне ромба:

в 1-й четверти: прямая $y = x + 1$ от $x > 0$

в 2-й четверти: $y = 1 — x$ от $x < 0$

в 3-й четверти: $y = x — 1$ от $x < 0$

в 4-й четверти: $y = -1 — x$ от $x > 0$

точки:
$(0, 1)$, $(-1, 2)$, $(1, 2)$, $(-2, -1)$, $(2, -3)$ — примеры на графике