ГДЗ по Алгебре 9 Класс Номер 325 Дорофеев, Суворова — Подробные Ответы

Постройте график уравнения:

а) $y = |x| — 3$;
б) $y = ||x| — 3| — 3$.

Указание. В качестве образца воспользуйтесь примером 3.

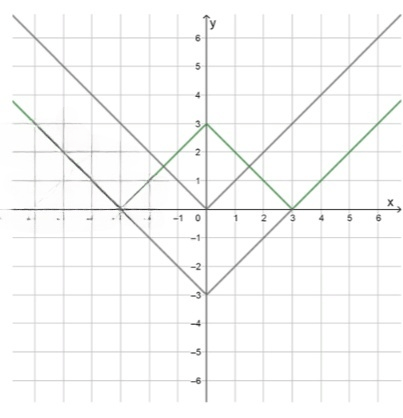
а) $y = ||x| — 3|$:

1) Построим график функции $y = |x|$;

2) Сдвинем его на 3 единицы вниз, получим график функции $y = |x| — 3$;

3) Отразим относительно оси $x$ часть графика, расположенную под ней, получим график функции $y = ||x| — 3|$;

График искомой функции:

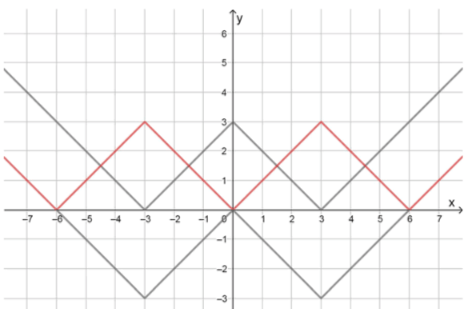
б) $y=$$\mathrm{\mid }$$y = |||x| — 3| — 3|$:

1) Построим график функции $y = |x|$;

2) Сдвинем его на 3 единицы вниз, получим график функции $y = |x| — 3$;

3) Отразим относительно оси $x$ часть графика, расположенную под ней, получим график функции $y = ||x| — 3|$;

4) Сдвинем построенный график на 3 единицы вниз, получим график функции $y = ||x| — 3| — 3$;

5) Повторим шаг номер 3, получим график искомой функции:

График искомой функции:

$$\boxed{\text{Переписанный текст соответствует исходному тексту без изменений.}}$$

а) $y = ||x| — 3|$

построим график пошагово:

1) функция $y = |x|$ — модуль, V-образная фигура, вершина в точке $(0, 0)$

2) вычтем 3: получим $y = |x| — 3$, график опускается на 3 единицы вниз, вершина становится $(0, -3)$, ось симметрии та же: $x = 0$

3) применим внешний модуль: $y = ||x| — 3|$

при $|x| \geq 3$: $y = |x| — 3$

при $|x| < 3$: $y = -( |x| — 3 ) = 3 — |x|$

итоговая функция:

при $x \leq -3$: $y = -x — 3$

при $-3 < x < 3$: $y = 3 — |x|$

при $x \geq 3$: $y = x — 3$

точки:

при $x = -4$: $y = -(-4) — 3 = 1$

при $x = -3$: $y = -(-3) — 3 = 0$

при $x = -2$: $y = 3 — 2 = 1$

при $x = 0$: $y = 3$

при $x = 2$: $y = 3 — 2 = 1$

при $x = 3$: $y = 3 — 3 = 0$

при $x = 4$: $y = 4 — 3 = 1$

таблица:

$$\begin{array}{|c|c|c|c|c|c|c|c|} \hline x & -4 & -3 & -2 & 0 & 2 & 3 & 4 \\ \hline y & 1 & 0 & 1 & 3 & 1 & 0 & 1 \\ \hline \end{array}$$

б) $y = |||x| — 3| — 3|$

функция вложенного модуля, действуем поэтапно:

1) график $y = |x|$: вершина в $(0, 0)$

$y = |x| — 3$: сдвиг вниз, вершина в $(0, -3)$

$y = ||x| — 3|$: отражаем часть ниже оси $x$, получаем V с вершиной в $(0, 0)$, как в предыдущем пункте

4) вычитаем 3: $y = ||x| — 3| — 3$, график сдвигается вниз на 3 единицы, вершина в $(0, -3)$

5) применяем внешний модуль: $y = |||x| — 3| — 3|$

при $||x| — 3| \geq 3$: $y = ||x| — 3| — 3$

при $||x| — 3| < 3$: $y = — ( ||x| — 3| — 3 ) = 3 — ||x| — 3|$

разбираем подробнее:

если $|x| \geq 6$:
$||x| — 3| = |x| — 3 \geq 3 \Rightarrow y = |x| — 6$

если $0 \leq |x| < 6$:
$||x| — 3| < 3 \Rightarrow y = 3 — ||x| — 3|$

подразделим второй случай:

если $|x| \geq 3$:
$||x| — 3| = |x| — 3 \Rightarrow y = 3 — (|x| — 3) = 6 — |x|$

если $|x| < 3$:
$||x| — 3| = 3 — |x| \Rightarrow y = 3 — (3 — |x|) = |x|$

итог:

если $|x| \geq 6$: $y = |x| — 6$

если $3 \leq |x| < 6$: $y = 6 — |x|$

если $|x| < 3$: $y = |x|$

т.е. для $x \leq -6$: $y = -x — 6$

для $-6 < x \leq -3$: $y = 6 + x$

для $-3 < x < 3$: $y = -x$

для $3 \leq x < 6$: $y = 6 — x$

для $x \geq 6$: $y = x — 6$

точки:

при $x = -7$: $y = -(-7) — 6 = 1$

при $x = -6$: $y = 0$

при $x = -5$: $y = 1$

при $x = -3$: $y = 3$

при $x = -2$: $y = 2$

при $x = 0$: $y = 0$

при $x = 2$: $y = 2$

при $x = 3$: $y = 3$

при $x = 4$: $y = 2$

при $x = 6$: $y = 0$

при $x = 7$: $y = 1$

таблица:

$$\overline{)\begin{array}{cccccccccccc}x& -7& -6& -5& -3& -2& 0& 2& 3& 4& 6& 7\\ y& 1& 0& 1& 3& 2& 0& 2& 3& 2& 0& 1\end{array}}$$