Краткий ответ:
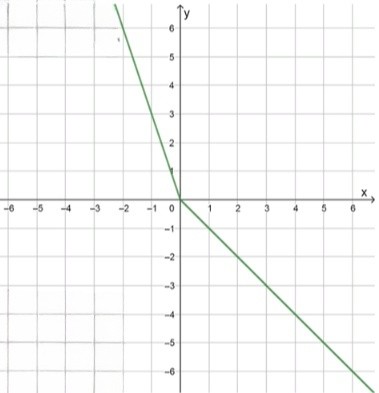
а) y = ∣ x ∣ − 2 x y = |x| — 2x
y = { − x , если x ≥ 0 ; − 3 x , если x < 0. y = \begin{cases} -x, & \text{если } x \geq 0; \\ -3x, & \text{если } x < 0. \end{cases}
1) y = − x y = -x
x 0 2 y 0 − 2 \begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 0 & -2 \\ \hline \end{array}
2) y = − 3 x y = -3x
x − 1 0 y 3 0 \begin{array}{|c|c|c|} \hline x & -1 & 0 \\ \hline y & 3 & 0 \\ \hline \end{array}
График искомой функции:
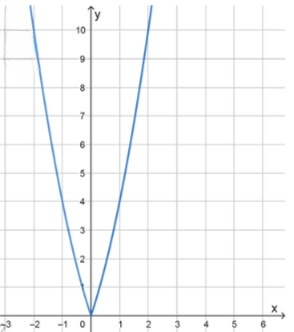
б) y = x 2 + 3 ∣ x ∣ y = x^2 + 3|x|
y = { x 2 + 3 x , если x ≥ 0 ; x 2 − 3 x , если x < 0. y = \begin{cases} x^2 + 3x, & \text{если } x \geq 0; \\ x^2 — 3x, & \text{если } x < 0. \end{cases}
1) y = x 2 + 3 x y = x^2 + 3x
x 0 1 2 y 0 4 10 \begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 2 \\ \hline y & 0 & 4 & 10 \\ \hline \end{array}
2) y = x 2 − 3 x y = x^2 — 3x
x − 2 − 1 0 y 10 4 0 \begin{array}{|c|c|c|c|} \hline x & -2 & -1 & 0 \\ \hline y & 10 & 4 & 0 \\ \hline \end{array}
График искомой функции:
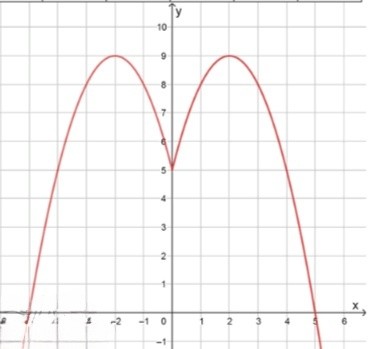
в) y = ( 5 − ∣ x ∣ ) ( ∣ x ∣ + 1 ) y = (5 — |x|)(|x| + 1)
y = ( 5 − ∣ x ∣ ) ( ∣ x ∣ + 1 ) = 5 ∣ x ∣ + 5 − ∣ x ∣ 2 − ∣ x ∣ = − ∣ x ∣ 2 + 4 ∣ x ∣ + 5 y = (5 — |x|)(|x| + 1) = 5|x| + 5 — |x|^2 — |x| = -|x|^2 + 4|x| + 5
y = { − x 2 + 4 x + 5 , если x ≥ 0 ; − x 2 − 4 x + 5 , если x < 0. y = \begin{cases} -x^2 + 4x + 5, & \text{если } x \geq 0; \\ -x^2 — 4x + 5, & \text{если } x < 0. \end{cases}
1) y = − x 2 + 4 x + 5 y = -x^2 + 4x + 5 x 0 = 2 x_0 = 2 y 0 = 9 y_0 = 9
x 0 1 3 4 5 y 5 8 8 5 0 \begin{array}{|c|c|c|c|c|c|} \hline x & 0 & 1 & 3 & 4 & 5 \\ \hline y & 5 & 8 & 8 & 5 & 0 \\ \hline \end{array}
2) y = − x 2 − 4 x + 5 y = -x^2 — 4x + 5 x 0 = − 2 x_0 = -2 y 0 = 9 y_0 = 9
x − 5 − 4 − 3 − 1 0 y 0 5 8 8 5 \begin{array}{|c|c|c|c|c|c|} \hline x & -5 & -4 & -3 & -1 & 0 \\ \hline y & 0 & 5 & 8 & 8 & 5 \\ \hline \end{array}
График искомой функции:
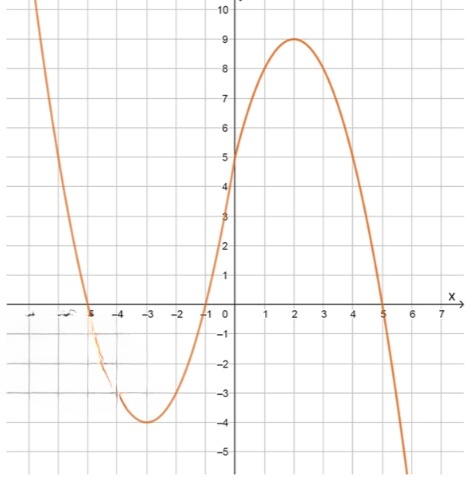
г) y = ( 5 − ∣ x ∣ ) ( x + 1 ) y = (5 — |x|)(x + 1)
y = 5 x + 5 − x ∣ x ∣ − ∣ x ∣ = { − x 2 + 4 x + 5 , если x ≥ 0 ; x 2 + 6 x + 5 , если x < 0. y = 5x + 5 — x|x| — |x| = \begin{cases} -x^2 + 4x + 5, & \text{если } x \geq 0; \\ x^2 + 6x + 5, & \text{если } x < 0. \end{cases}
1) y = − x 2 + 4 x + 5 y = -x^2 + 4x + 5 x 0 = 2 x_0 = 2 y 0 = 9 y_0 = 9
x 0 1 3 4 5 6 y 5 8 8 5 0 − 6 \begin{array}{|c|c|c|c|c|c|c|} \hline x & 0 & 1 & 3 & 4 & 5 & 6 \\ \hline y & 5 & 8 & 8 & 5 & 0 & -6 \\ \hline \end{array}
2) y = x 2 + 6 x + 5 y = x^2 + 6x + 5 x 0 = − 3 x_0 = -3 y 0 = − 4 y_0 = -4
x − 7 − 6 − 5 − 4 − 2 − 1 0 y 11 5 0 − 3 − 3 0 5 \begin{array}{|c|c|c|c|c|c|c|} \hline x & -7 & -6 & -5 & -4 & -2 & -1 & 0 \\ \hline y & 11 & 5 & 0 & -3 & -3 & 0 & 5 \\ \hline \end{array}
График искомой функции:
д) y = 1 ∣ x ∣ − 3 y = \frac{1}{|x| — 3}
y = { 1 x − 3 , x > 0 ; 1 − x − 3 , x < 0. y = \begin{cases} \frac{1}{x — 3}, & x > 0; \\ \frac{1}{-x — 3}, & x < 0. \end{cases}
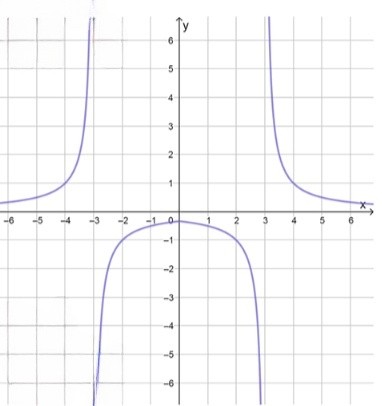
График искомой функции:
Подробный ответ:
а) y = ∣ x ∣ − 2 x y = |x| — 2x
при x ≥ 0 x \geq 0 ∣ x ∣ = x |x| = x y = x − 2 x = − x y = x — 2x = -x
при x < 0 x < 0 ∣ x ∣ = − x |x| = -x y = − x − 2 x = − 3 x y = -x — 2x = -3x
функция кусочно-линейная, из двух прямых:
первая прямая: y = − x y = -x x ≥ 0 x \geq 0 ( 0 , 0 ) (0, 0) ( 2 , − 2 ) (2, -2)
вторая прямая: y = − 3 x y = -3x x < 0 x < 0 ( − 1 , 3 ) (-1, 3) ( 0 , 0 ) (0, 0)
таблицы значений:
x 0 2 y 0 − 2 x − 1 0 y 3 0 \begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 0 & -2 \\ \hline \end{array} \quad \begin{array}{|c|c|c|} \hline x & -1 & 0 \\ \hline y & 3 & 0 \\ \hline \end{array}
б) y = x 2 + 3 ∣ x ∣ y = x^2 + 3|x|
при x ≥ 0 x \geq 0 y = x 2 + 3 x y = x^2 + 3x
при x < 0 x < 0 y = x 2 − 3 x y = x^2 — 3x
обе части — параболы с ветвями вверх
первая: y = x 2 + 3 x y = x^2 + 3x x = − 3 2 x = -\frac{3}{2} x ≥ 0 x \geq 0 ( 0 , 0 ) (0, 0) ( 1 , 4 ) (1, 4) ( 2 , 10 ) (2, 10)
вторая: y = x 2 − 3 x y = x^2 — 3x x = 3 2 x = \frac{3}{2} x < 0 x < 0 ( − 2 , 10 ) (-2, 10) ( − 1 , 4 ) (-1, 4) ( 0 , 0 ) (0, 0)
таблицы значений:
x 0 1 2 y 0 4 10 x − 2 − 1 0 y 10 4 0 \begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 2 \\ \hline y & 0 & 4 & 10 \\ \hline \end{array} \quad \begin{array}{|c|c|c|} \hline x & -2 & -1 & 0 \\ \hline y & 10 & 4 & 0 \\ \hline \end{array}
в) y = ( 5 − ∣ x ∣ ) ( ∣ x ∣ + 1 ) y = (5 — |x|)(|x| + 1)
раскроем скобки:y = 5 ∣ x ∣ + 5 − ∣ x ∣ 2 − ∣ x ∣ = − ∣ x ∣ 2 + 4 ∣ x ∣ + 5 y = 5|x| + 5 — |x|^2 — |x| = -|x|^2 + 4|x| + 5
при x ≥ 0 x \geq 0 y = − x 2 + 4 x + 5 y = -x^2 + 4x + 5
при x < 0 x < 0 y = − x 2 − 4 x + 5 y = -x^2 — 4x + 5
обе — параболы с ветвями вниз
первая: вершина x = 2 x = 2 y = − 4 + 8 + 5 = 9 y = -4 + 8 + 5 = 9
вторая: вершина x = − 2 x = -2 y = − 4 + 8 + 5 = 9 y = -4 + 8 + 5 = 9
таблицы значений:
x 0 1 3 4 5 y 5 8 8 5 0 x − 5 − 4 − 3 − 1 0 y 0 5 8 8 5 \begin{array}{|c|c|c|c|c|c|} \hline x & 0 & 1 & 3 & 4 & 5 \\ \hline y & 5 & 8 & 8 & 5 & 0 \\ \hline \end{array} \quad \begin{array}{|c|c|c|c|c|c|} \hline x & -5 & -4 & -3 & -1 & 0 \\ \hline y & 0 & 5 & 8 & 8 & 5 \\ \hline \end{array}
г) y = ( 5 − ∣ x ∣ ) ( x + 1 ) y = (5 — |x|)(x + 1)
раскрываем:y = 5 x + 5 − x ∣ x ∣ − ∣ x ∣ y = 5x + 5 — x|x| — |x|
при x ≥ 0 x \geq 0 y = 5 x + 5 − x 2 − x = − x 2 + 4 x + 5 y = 5x + 5 — x^2 — x = -x^2 + 4x + 5
при x < 0 x < 0 y = 5 x + 5 + x 2 + x = x 2 + 6 x + 5 y = 5x + 5 + x^2 + x = x^2 + 6x + 5
первая — парабола с вершиной x = 2 x = 2 y = − 4 + 8 + 5 = 9 y = -4 + 8 + 5 = 9
вторая — парабола с вершиной x = − 3 x = -3 y = 9 − 18 + 5 = − 4 y = 9 — 18 + 5 = -4
таблицы значений:
x 0 1 3 4 5 6 y 5 8 8 5 0 − 6 x − 7 − 6 − 5 − 4 − 2 − 1 0 y 11 5 0 − 3 − 3 0 5 \begin{array}{|c|c|c|c|c|c|c|} \hline x & 0 & 1 & 3 & 4 & 5 & 6 \\ \hline y & 5 & 8 & 8 & 5 & 0 & -6 \\ \hline \end{array} \quad \begin{array}{|c|c|c|c|c|c|c|} \hline x & -7 & -6 & -5 & -4 & -2 & -1 & 0 \\ \hline y & 11 & 5 & 0 & -3 & -3 & 0 & 5 \\ \hline \end{array}
д) y = 1 ∣ x ∣ − 3 y = \frac{1}{|x| — 3}
область определения: ∣ x ∣ ≠ 3 ⇒ x ≠ ± 3 |x| \ne 3 \Rightarrow x \ne \pm 3
при x > 0 x > 0 y = 1 x − 3 y = \frac{1}{x — 3}
при x < 0 x < 0 y = 1 − x − 3 y = \frac{1}{-x — 3}
функция разрывна в точках x = 3 x = 3 x = − 3 x = -3
таблицы значений:
x 0 1 2 2.5 3.5 4 5 y − 1 3 − 0.5 − 1 − 2 2 1 0.5 x − 5 − 4 − 3.5 − 2.5 − 2 − 1 0 y 0.5 1 2 − 2 − 1 − 0.5 − 1 3 \begin{array}{|c|c|c|c|c|c|c|} \hline x & 0 & 1 & 2 & 2.5 & 3.5 & 4 & 5 \\ \hline y & -\frac{1}{3} & -0.5 & -1 & -2 & 2 & 1 & 0.5 \\ \hline \end{array} \quad \begin{array}{|c|c|c|c|c|c|c|} \hline x & -5 & -4 & -3.5 & -2.5 & -2 & -1 & 0 \\ \hline y & 0.5 & 1 & 2 & -2 & -1 & -0.5 & -\frac{1}{3} \\ \hline \end{array}





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!