ГДЗ по Алгебре 9 Класс Номер 323 Дорофеев, Суворова — Подробные Ответы

Постройте график уравнения (323–326).

а) $y=\mathrm{\mid }2x-4\mathrm{\mid }$;
б) $y=\mathrm{\mid }{x}^2-3\mathrm{\mid }$;
в) $y=\mathrm{\mid }{x}^2-x-2\mathrm{\mid }$;
г) $y=\frac{6}{\mathrm{\mid }x\mathrm{\mid }}$;
д) $y=\frac{1}{\mathrm{\mid }x-3\mathrm{\mid }}$.

а) $y=\mathrm{\mid }2x-4\mathrm{\mid }$:

1) Построим график функции $y=2x-4$:

$$\overline{)\begin{array}{ccc}x& 0& 2\\ y& -4& 0\end{array}}$$

2) График искомой функции:

б) $y=\mathrm{\mid }{x}^2-3\mathrm{\mid }$:

1) Построим график функции $y=x^2-3$:

$x_0=0$ и $y_0=-3$;

$$\overline{)\begin{array}{ccccc}x& -3& -1& 1& 3\\ y& 6& -2& -2& 6\end{array}}$$

2) График искомой функции:

в) $y=\mathrm{\mid }{x}^2-x-2\mathrm{\mid }$:

1) Построим график функции $y=x^2-x-2$:

$x_0=-\frac{-1}{2}=\frac{1}{2}$ и $y_0=\frac{1}{4}-\frac{1}{2}-2=-2\frac{1}{4}$;

$$\overline{)\begin{array}{ccccc}x& -3& -1& 1& 3\\ y& 6& -2& -2& 6\end{array}}$$

2) График искомой функции:

г) $y=\frac{6}{\mathrm{\mid }x\mathrm{\mid }}$:

1) Построим график функции $y=\frac{6}{x}$:

$$\overline{)\begin{array}{ccccccccc}x& -6& -3& -2& -1& 1& 2& 3& 6\\ y& -1& -2& -3& -6& 6& 3& 2& 1\end{array}}$$

2) График искомой функции:

д) $y=\frac{1}{\mathrm{\mid }x-3\mathrm{\mid }}$:

1) Построим график функции $y=\frac{1}{x-3}$:

$x_0=3$ и $y_0=0$;

$$\overline{)\begin{array}{ccccccc}x& 1& 2& 2,5& 3,5& 4& 5\\ y& -0,5& -1& -2& 2& 1& 0,5\end{array}}$$

2) График искомой функции:

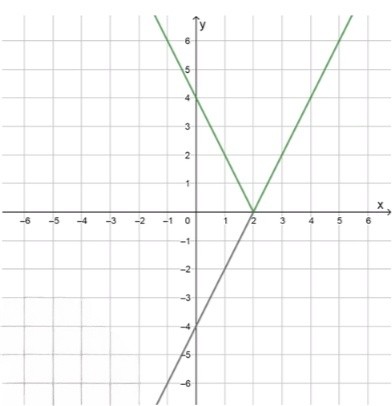
а) $y=\mathrm{\mid }2x-4\mathrm{\mid }$

построим график функции $y=2x-4$, это линейная функция с угловым коэффициентом 2 и свободным членом -4. график — прямая, проходящая через точку $(0,-4)$, и пересекающая ось $x$ в точке, где $2x-4=0\Rightarrow x=2$

при $x<2$, выражение $2x-4<0$, значит модуль раскрывается с минусом:
$y=-(2x-4)=-2x+4$

при $x\ge 2$, $y=2x-4$

точки для построения графика исходной линейной функции:

$$\overline{)\begin{array}{ccc}x& 0& 2\\ y& -4& 0\end{array}}$$

график функции $y=\mathrm{\mid }2x-4\mathrm{\mid }$ представляет собой “угол”, симметричный относительно прямой $x=2$

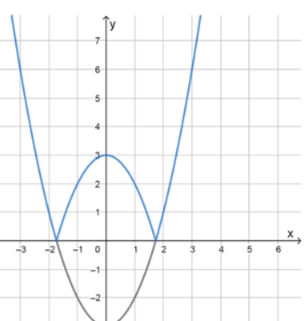
б) $y=\mathrm{\mid }{x}^2-3\mathrm{\mid }$

функция $x^2-3$ — парабола с вершиной в точке $(0,-3)$. её ветви направлены вверх, поскольку коэффициент при $x^2$ положительный

модуль преобразует все отрицательные значения в положительные, поэтому участок графика ниже оси $x$ отражается симметрично вверх

рассчитаем значения:

$$\overline{)\begin{array}{cccccc}x& -3& -1& 0& 1& 3\\ x^2-3& 6& -2& -3& -2& 6\\ y=\mathrm{\mid }{x}^2-3\mathrm{\mid }& 6& 2& 3& 2& 6\end{array}}$$

$$\begin{array}{|c|c|c|c|c|} \hline x & -3 & -1 & 0 & 1 & 3 \\ \hline x^2 — 3 & 6 & -2 & -3 & -2 & 6 \\ \hline y = |x^2 — 3| & 6 & 2 & 3 & 2 & 6 \\ \hline \end{array}$$

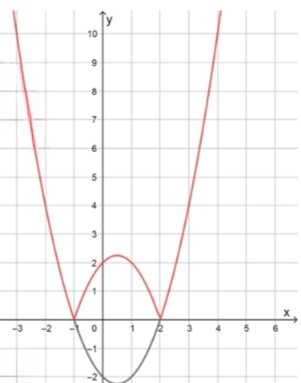
в) $y=\mathrm{\mid }{x}^2-x-2\mathrm{\mid }$

преобразуем:
$x^2-x-2=(x-2)(x+1)$

это парабола с ветвями вверх, нули функции — точки $x=-1$ и $x=2$

на интервалах:

при $x<-1$, выражение положительно
при $-1<x<2$, выражение отрицательно
при $x>2$, снова положительно

модуль изменит знак на интервале $(-1;2)$, при этом график в этой области будет отражён вверх

найдём вершину:
$x_0=\frac{-(-1)}{2\cdot 1}=\frac{1}{2}$
$y_0={\left(\frac{1}{2}\right)}^2-\frac{1}{2}-2=\frac{1}{4}-\frac{1}{2}-2=-\frac{9}{4}$

точки:

$$\overline{)\begin{array}{cccccc}x& -3& -1& 1& 2& 3\\ x^2-x-2& 10& 0& -2& 0& 4\\ y=\mathrm{\mid }{x}^2-x-2\mathrm{\mid }& 10& 0& 2& 0& 4\end{array}}$$

г) $y=\frac{6}{\mathrm{\mid }x\mathrm{\mid }}$

функция определяется при всех $x\mathrm{\ne }0$. знаменатель не может равняться нулю, значит $x\mathrm{\ne }0$

модуль в знаменателе делает график симметричным относительно оси $y$

значения:

$$\overline{)\begin{array}{ccccccccc}x& -6& -3& -2& -1& 1& 2& 3& 6\\ y& 1& 2& 3& 6& 6& 3& 2& 1\end{array}}$$

график состоит из двух ветвей гиперболы в первой и второй четвертях

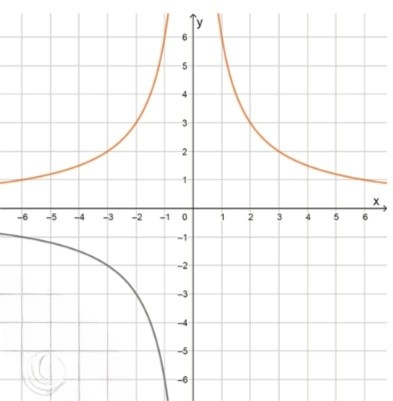
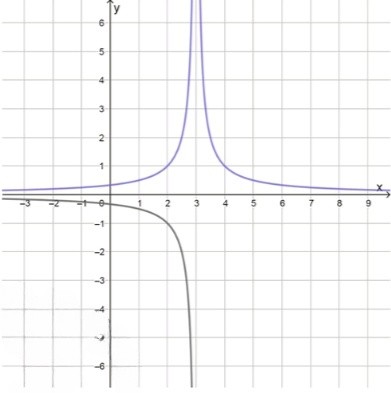
д) $y=\frac{1}{\mathrm{\mid }x-3\mathrm{\mid }}$

модуль в знаменателе делает график симметричным относительно вертикали $x=3$

функция не определена при $x=3$, так как знаменатель обращается в ноль. в этой точке — вертикальная асимптота

значения:

$$\overline{)\begin{array}{ccccccc}x& 1& 2& 2.5& 3.5& 4& 5\\ x-3& -2& -1& -0.5& 0.5& 1& 2\\ \mathrm{\mid }x-3\mathrm{\mid }& 2& 1& 0.5& 0.5& 1& 2\\ y& 0.5& 1& 2& 2& 1& 0.5\end{array}}$$

график — гипербола, симметричная относительно вертикальной прямой $x=3$, расположена в первой и второй четвертях, с вертикальной асимптотой $x=3$

$x = 3$