
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 322 Дорофеев, Суворова — Подробные Ответы
Найдите асимптоты графика функции и изобразите этот график схематически:
а) ;
б) ;
в) .
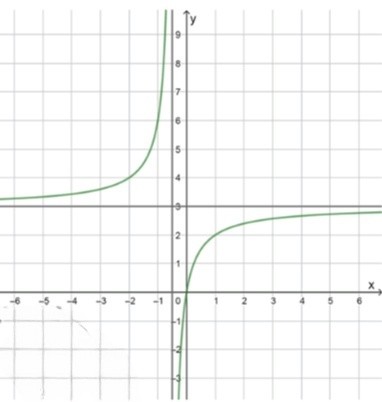
а)
Вертикальная асимптота:
Горизонтальная асимптота:
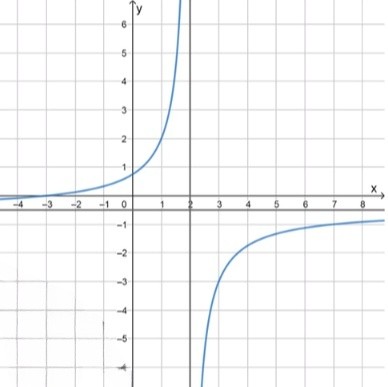
б)
Вертикальная асимптота:
Горизонтальная асимптота:
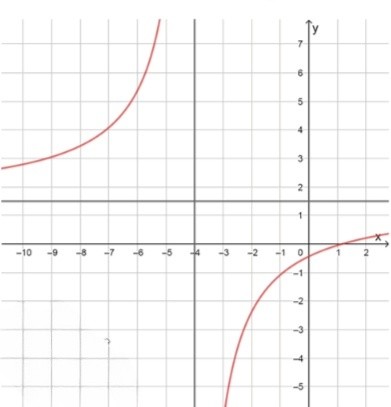
в)
Вертикальная асимптота:
Горизонтальная асимптота:
а)
функция представлена в виде разности константы и дроби , которая при стремится к нулю. значит, при удалении от начала координат график приближается к горизонтальной прямой , которая является горизонтальной асимптотой
вертикальная асимптота получается из условия, при котором знаменатель обращается в ноль:
вертикальная асимптота:
горизонтальная асимптота:
б)
представим функцию как сумму постоянной части и дробной . при дробная часть стремится к нулю, значит график приближается к прямой
вертикальная асимптота находится из уравнения знаменателя:
вертикальная асимптота:
горизонтальная асимптота:
в)
представлено как разность константы и дроби . при дробь стремится к нулю, значит график приближается к прямой
найдём вертикальную асимптоту, приравняв знаменатель к нулю:
вертикальная асимптота:
горизонтальная асимптота:




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!