Задача
Постройте график функции:
а) y = x + 4 x + 2 y = \frac{x + 4}{x + 2}
б) y = 3 − x x − 1 y = \frac{3 — x}{x — 1}
в) y = x + 1 x + 2 y = \frac{x + 1}{x + 2}
Совет. В качестве образца воспользуйтесь примером 4, разобраным в тексте.
Краткий ответ:
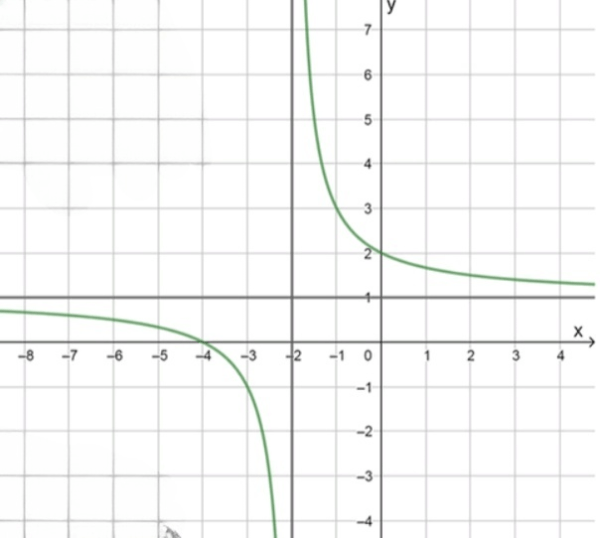
а) y = x + 4 x + 2 y = \frac{x + 4}{x + 2}
y = x + 4 x + 2 = ( x + 2 ) + 2 x + 2 = 1 + 2 x + 2 y = \frac{x + 4}{x + 2} = \frac{(x + 2) + 2}{x + 2} = 1 + \frac{2}{x + 2}
Вертикальная асимптота: x = − 2 x = -2 Горизонтальная асимптота: y = 1 y = 1 x x − 6 -6 − 4 -4 − 3 -3 − 2 1 2 -2 \frac{1}{2} − 1 1 2 -1 \frac{1}{2} 0 0 2 2 y y 1 2 \frac{1}{2} 0 0 − 1 -1 − 3 -3 5 5 3 3 1 1 2 1 \frac{1}{2}
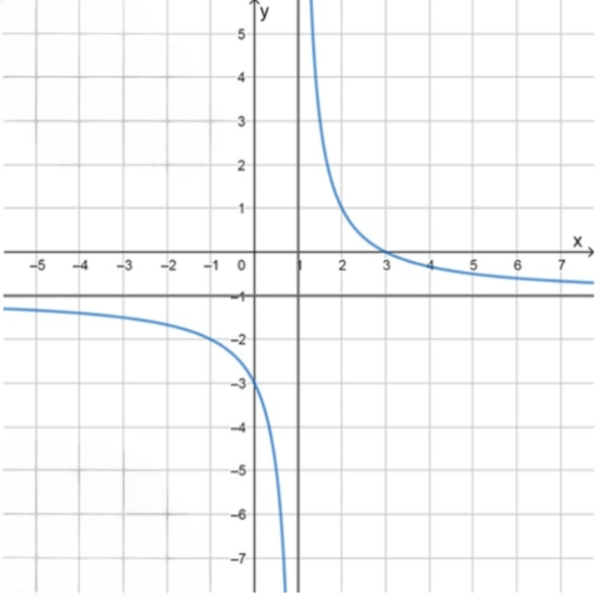
б) y = 3 − x x − 1 y = \frac{3 — x}{x — 1}
y = 3 − x x − 1 = − ( x − 1 ) + 2 x − 1 = − 1 + 2 x − 1 y = \frac{3 — x}{x — 1} = \frac{-(x — 1) + 2}{x — 1} = -1 + \frac{2}{x — 1}
Вертикальная асимптота: x = 1 x = 1 Горизонтальная асимптота: y = − 1 y = -1 x x − 3 -3 − 1 -1 0 0 1 2 \frac{1}{2} 1 1 2 1 \frac{1}{2} 2 2 3 3 5 5 y y − 1 1 2 -1 \frac{1}{2} − 2 -2 − 3 -3 − 5 -5 3 3 1 1 0 0 − 1 2 -\frac{1}{2}
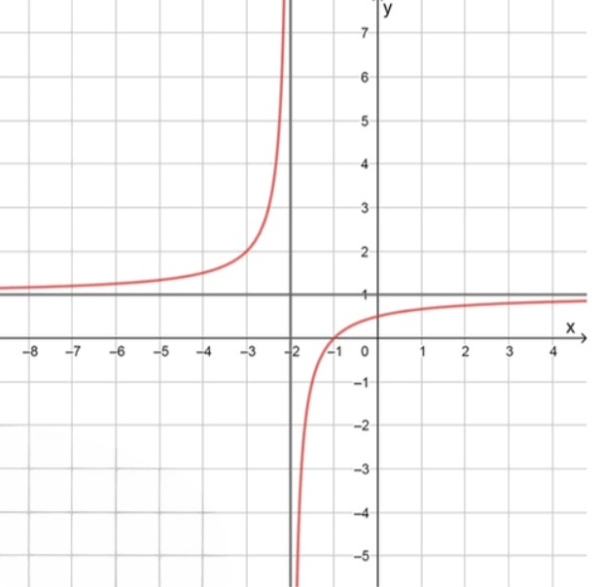
в) y = x + 1 x + 2 y = \frac{x + 1}{x + 2}
y = x + 1 x + 2 = ( x + 2 ) − 1 x + 2 = 1 − 1 x + 2 y = \frac{x + 1}{x + 2} = \frac{(x + 2) — 1}{x + 2} = 1 — \frac{1}{x + 2}
Вертикальная асимптота: x = − 2 x = -2 Горизонтальная асимптота: y = 1 y = 1 x x − 4 -4 − 3 -3 − 2 1 2 -2 \frac{1}{2} − 1 1 2 -1 \frac{1}{2} − 1 -1 0 0 y y 1 1 2 1 \frac{1}{2} 2 2 3 3 − 1 -1 0 0 1 2 \frac{1}{2}
Подробный ответ:
а) y = x + 4 x + 2 y = \frac{x + 4}{x + 2}
y = x + 4 x + 2 = ( x + 2 ) + 2 x + 2 = x + 2 x + 2 + 2 x + 2 = 1 + 2 x + 2 y = \frac{x + 4}{x + 2} = \frac{(x + 2) + 2}{x + 2} = \frac{x + 2}{x + 2} + \frac{2}{x + 2} = 1 + \frac{2}{x + 2}
выражение представлено как сумма постоянного члена и дроби. постоянный член определяет горизонтальную асимптоту, дробная часть — отклонение от неё.
вертикальная асимптота — значение x x x + 2 = 0 ⇒ x = − 2 x + 2 = 0 \Rightarrow x = -2
горизонтальная асимптота находится как предел функции при x → ∞ x \to \infty x → − ∞ x \to -\infty lim x → ± ∞ ( 1 + 2 x + 2 ) = 1 \lim_{x \to \pm\infty} \left( 1 + \frac{2}{x + 2} \right) = 1
найдём значения функции при некоторых x x
при x = − 6 x = -6 y = − 6 + 4 − 6 + 2 = − 2 − 4 = 1 2 y = \frac{-6 + 4}{-6 + 2} = \frac{-2}{-4} = \frac{1}{2} x = − 4 x = -4 y = − 4 + 4 − 4 + 2 = 0 − 2 = 0 y = \frac{-4 + 4}{-4 + 2} = \frac{0}{-2} = 0 x = − 3 x = -3 y = − 3 + 4 − 3 + 2 = 1 − 1 = − 1 y = \frac{-3 + 4}{-3 + 2} = \frac{1}{-1} = -1 x = − 2.5 x = -2.5 y = − 2.5 + 4 − 2.5 + 2 = 1.5 − 0.5 = − 3 y = \frac{-2.5 + 4}{-2.5 + 2} = \frac{1.5}{-0.5} = -3 x = − 1.5 x = -1.5 y = − 1.5 + 4 − 1.5 + 2 = 2.5 0.5 = 5 y = \frac{-1.5 + 4}{-1.5 + 2} = \frac{2.5}{0.5} = 5 x = 0 x = 0 y = 0 + 4 0 + 2 = 4 2 = 2 y = \frac{0 + 4}{0 + 2} = \frac{4}{2} = 2 x = 2 x = 2 y = 2 + 4 2 + 2 = 6 4 = 3 2 = 1 1 2 y = \frac{2 + 4}{2 + 2} = \frac{6}{4} = \frac{3}{2} = 1 \frac{1}{2}
таблица:
x x − 6 -6 − 4 -4 − 3 -3 − 2.5 -2.5 − 1.5 -1.5 0 0 2 2 y y 1 2 \frac{1}{2} 0 0 − 1 -1 − 3 -3 5 5 2 2 1 1 2 1 \frac{1}{2}
б) y = 3 − x x − 1 y = \frac{3 — x}{x — 1}
преобразуем числитель:y = 3 − x x − 1 = − ( x − 3 ) x − 1 = − ( x − 1 + 2 ) x − 1 = − ( x − 1 ) − 2 x − 1 = − 1 − 2 x − 1 y = \frac{3 — x}{x — 1} = \frac{-(x — 3)}{x — 1} = \frac{-(x — 1 + 2)}{x — 1} = \frac{-(x — 1) — 2}{x — 1} = -1 — \frac{2}{x — 1}
функция представлена как сумма постоянной и дробной части
вертикальная асимптота: x = 1 x = 1
горизонтальная асимптота — предел при x → ± ∞ x \to \pm\infty lim x → ± ∞ ( − 1 − 2 x − 1 ) = − 1 \lim_{x \to \pm\infty} \left( -1 — \frac{2}{x — 1} \right) = -1
подставим значения:
при x = − 3 x = -3 y = 3 − ( − 3 ) − 3 − 1 = 6 − 4 = − 1.5 = − 1 1 2 y = \frac{3 — (-3)}{-3 — 1} = \frac{6}{-4} = -1.5 = -1 \frac{1}{2} x = − 1 x = -1 y = 3 + 1 − 1 − 1 = 4 − 2 = − 2 y = \frac{3 + 1}{-1 — 1} = \frac{4}{-2} = -2 x = 0 x = 0 y = 3 − 1 = − 3 y = \frac{3}{-1} = -3 x = 0.5 x = 0.5 y = 3 − 0.5 0.5 − 1 = 2.5 − 0.5 = − 5 y = \frac{3 — 0.5}{0.5 — 1} = \frac{2.5}{-0.5} = -5 x = 1.5 x = 1.5 y = 3 − 1.5 1.5 − 1 = 1.5 0.5 = 3 y = \frac{3 — 1.5}{1.5 — 1} = \frac{1.5}{0.5} = 3 x = 2 x = 2 y = 3 − 2 2 − 1 = 1 1 = 1 y = \frac{3 — 2}{2 — 1} = \frac{1}{1} = 1 x = 3 x = 3 y = 3 − 3 3 − 1 = 0 2 = 0 y = \frac{3 — 3}{3 — 1} = \frac{0}{2} = 0 x = 5 x = 5 y = 3 − 5 5 − 1 = − 2 4 = − 1 2 y = \frac{3 — 5}{5 — 1} = \frac{-2}{4} = -\frac{1}{2}
таблица:
x x − 3 -3 − 1 -1 0 0 0.5 0.5 1.5 1.5 2 2 3 3 5 5 y y − 1 1 2 -1 \frac{1}{2} − 2 -2 − 3 -3 − 5 -5 3 3 1 1 0 0 − 1 2 -\frac{1}{2}
в) y = x + 1 x + 2 y = \frac{x + 1}{x + 2}
y = x + 1 x + 2 = ( x + 2 ) − 1 x + 2 = x + 2 x + 2 − 1 x + 2 = 1 − 1 x + 2 y = \frac{x + 1}{x + 2} = \frac{(x + 2) — 1}{x + 2} = \frac{x + 2}{x + 2} — \frac{1}{x + 2} = 1 — \frac{1}{x + 2}
вертикальная асимптота — знаменатель обращается в ноль:x + 2 = 0 ⇒ x = − 2 x + 2 = 0 \Rightarrow x = -2
горизонтальная асимптота:lim x → ± ∞ ( 1 − 1 x + 2 ) = 1 \lim_{x \to \pm\infty} \left( 1 — \frac{1}{x + 2} \right) = 1
подставим значения:
при x = − 4 x = -4 y = − 4 + 1 − 4 + 2 = − 3 − 2 = 1.5 = 1 1 2 y = \frac{-4 + 1}{-4 + 2} = \frac{-3}{-2} = 1.5 = 1 \frac{1}{2} x = − 3 x = -3 y = − 3 + 1 − 3 + 2 = − 2 − 1 = 2 y = \frac{-3 + 1}{-3 + 2} = \frac{-2}{-1} = 2 x = − 2.5 x = -2.5 y = − 2.5 + 1 − 2.5 + 2 = − 1.5 − 0.5 = 3 y = \frac{-2.5 + 1}{-2.5 + 2} = \frac{-1.5}{-0.5} = 3 x = − 1.5 x = -1.5 y = − 1.5 + 1 − 1.5 + 2 = − 0.5 0.5 = − 1 y = \frac{-1.5 + 1}{-1.5 + 2} = \frac{-0.5}{0.5} = -1 x = − 1 x = -1 y = − 1 + 1 − 1 + 2 = 0 1 = 0 y = \frac{-1 + 1}{-1 + 2} = \frac{0}{1} = 0 x = 0 x = 0 y = 0 + 1 0 + 2 = 1 2 y = \frac{0 + 1}{0 + 2} = \frac{1}{2}
таблица:
x x − 4 -4 − 3 -3 − 2.5 -2.5 − 1.5 -1.5 − 1 -1 0 0 y y 1 1 2 1 \frac{1}{2} 2 2 3 3 − 1 -1 0 0 1 2 \frac{1}{2}





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!