ГДЗ по Алгебре 9 Класс Номер 319 Дорофеев, Суворова — Подробные Ответы

Постройте в координатной плоскости асимптоты графика заданной функции и изобразите этот график схематически:

а) $y=\frac{1}{x+3}-2$;

б) $y=-\frac{3}{x+4}+6$;

в) $y=\frac{2}{x-1}-4$;

г) $y=-\frac{6}{x-3}-2$.

В каждом случае найдите координаты точек пересечения графика с осью $x$ и осью $y$ и отметьте эти точки на рисунке.

а) $y=\frac{1}{x+3}-2$:

1) Вертикальная асимптота: $x=-3$;

2) Горизонтальная асимптота: $y=-2$;

3) Пересечение с осью $x$:
$\frac{1}{x+3}-2=0;$
$\frac{1}{x+3}=2;$
$2(x+3)=1;$
$2x+6=1;$
$2x=-5,\text{ отсюда }x=-2\frac{1}{2};$

4) Пересечение с осью $y$:
$y=\frac{1}{0+3}-2=\frac{1}{3}-2=-1\frac{2}{3};$

5) Схематический рисунок:$y = \frac{1}{x + 3} — 2$

б) $y=-\frac{3}{x+4}+6$:

1) Вертикальная асимптота: $x=-4$;

2) Горизонтальная асимптота: $y=6$;

3) Пересечение с осью $x$:
$-\frac{3}{x+4}+6=0;$
$-\frac{3}{x+4}=-6;$
$6(x+4)=3;$
$6x+24=3;$
$6x=-21,\text{ отсюда }x=-3\frac{1}{2};$

4) Пересечение с осью $y$:
$y=-\frac{3}{0+4}+6=-\frac{3}{4}+6=5\frac{1}{4};$

5) Схематический рисунок:$y = -\frac{3}{x + 4} + 6$

в) $y=\frac{2}{x-1}-4$:

1) Вертикальная асимптота: $x=1$;

2) Горизонтальная асимптота: $y=-4$;

3) Пересечение с осью $x$:
$\frac{2}{x-1}-4=0;$
$\frac{2}{x-1}=4;$
$4(x-1)=2;$
$4x-4=2;$
$4x=6,\text{ отсюда }x=1\frac{1}{2};$

4) Пересечение с осью $y$:
$y=\frac{2}{0-1}-4=-2-4=-6;$

5) Схематический рисунок:$y = \frac{2}{x — 1} — 4$

г) $y=-\frac{6}{x-3}-2$:

1) Вертикальная асимптота: $x=3$;

2) Горизонтальная асимптота: $y=-2$;

3) Пересечение с осью $x$:
$-\frac{6}{x-3}-2=0;$
$-\frac{6}{x-3}=2;$
$2(x-3)=-6;$
$2x-6=-6;$
$2x=0,\text{ отсюда }x=0;$

4) Пересечение с осью $y$:
$y=-\frac{6}{0-3}-2=2-2=0;$

5) Схематический рисунок:

$\boxed{\text{Графики построены и описаны выше.}}$

а) $y=\frac{1}{x+3}-2$

Вертикальная асимптота находится из условия, при котором знаменатель дроби обращается в ноль. Поскольку дробь имеет вид $\frac{1}{x+3}$, то выражение $x+3=0$ приводит к разрыву графика. Решим это уравнение:
$x+3=0\Rightarrow x=-3$.
Следовательно, вертикальная асимптота: $x=-3$.

Горизонтальная асимптота у функции вида $y=\frac{1}{x+a}+b$ находится как предел функции при $x\to \mathrm{\infty }$ или $x\to -\mathrm{\infty }$. Так как при больших по модулю $x$, дробная часть стремится к нулю:
${\lim }_{x\to \pm \mathrm{\infty }}\frac{1}{x+3}=0$,
тогда
$y=0-2=-2$.
Горизонтальная асимптота: $y=-2$.

Найдём точку пересечения графика с осью $x$, то есть найдём такие $x$, при которых $y=0$:
$\frac{1}{x+3}-2=0$
$\frac{1}{x+3}=2$
Домножим обе части на $x+3$:
$1=2(x+3)$
Раскроем скобки:
$1=2x+6$
Вычтем 6:
$-5=2x$
Разделим обе части на 2:
$x=-\frac{5}{2}=-2\frac{1}{2}$

Найдём точку пересечения с осью $y$, для этого подставим $x=0$:
$y=\frac{1}{0+3}-2=\frac{1}{3}-2=-\frac{5}{3}=-1\frac{2}{3}$

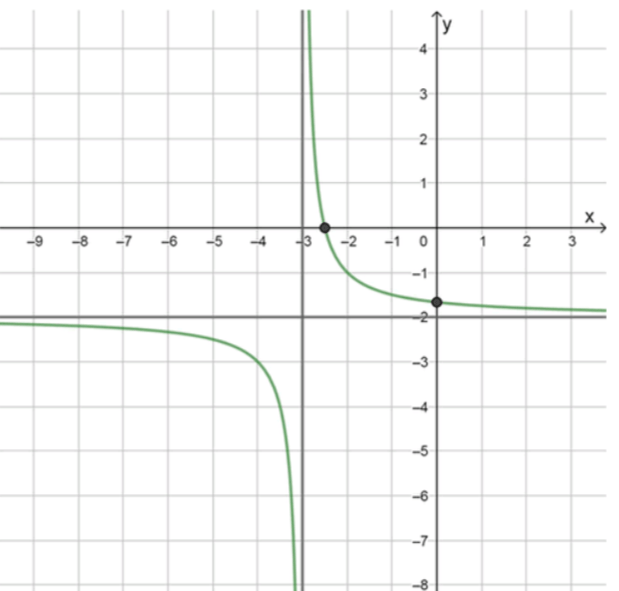
Форма графика:

Функция $y=\frac{1}{x+3}-2$ представляет собой гиперболу, смещённую относительно стандартной $y=\frac{1}{x}$ на 3 единицы влево и на 2 единицы вниз.
Её асимптоты: вертикальная $x=-3$, горизонтальная $y=-2$.
График состоит из двух ветвей:
— при $x<-3$, функция отрицательная и убывает от 0 до минус бесконечности при приближении к $x=-3$ справа;
— при $x>-3$, функция положительная и убывает от плюс бесконечности до 0 при удалении от асимптоты.
График имеет точку пересечения с осью $x$ при $x=-2\frac{1}{2}$, и с осью $y$ при $y=-1\frac{2}{3}$.

б) $y=-\frac{3}{x+4}+6$

Вертикальная асимптота: знаменатель $x+4=0\Rightarrow x=-4$

Горизонтальная асимптота: дробь стремится к нулю при больших $\mathrm{\mid }x\mathrm{\mid }$, а значит
$y=-0+6=6$

Пересечение с осью $x$, при $y=0$:
$-\frac{3}{x+4}+6=0\Rightarrow -\frac{3}{x+4}=-6\Rightarrow \frac{3}{x+4}=6\Rightarrow 3=6(x+4)\Rightarrow 3=$

$6x+24\Rightarrow 6x=-21\Rightarrow x=-\frac{7}{2}=-3\frac{1}{2}$

Пересечение с осью $y$, при $x=0$:
$y=-\frac{3}{0+4}+6=-\frac{3}{4}+6=\frac{21}{4}=5\frac{1}{4}$

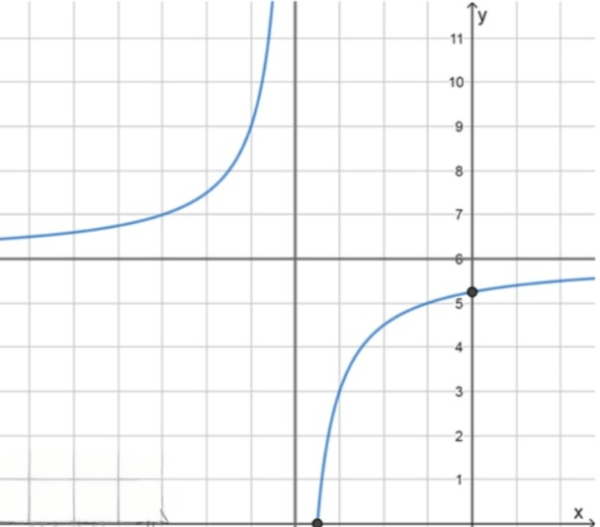
Форма графика:

График функции $y=-\frac{3}{x+4}+6$ — это отражённая и сдвинутая гипербола.
Асимптоты: $x=-4$, $y=6$
Точки пересечения: с осью $x$: $x=-3\frac{1}{2}$, с осью $y$: $y=5\frac{1}{4}$

в) $y=\frac{2}{x-1}-4$

Вертикальная асимптота:
$x-1=0\Rightarrow x=1$

Горизонтальная асимптота:
${\lim }_{x\to \pm \mathrm{\infty }}\frac{2}{x-1}=0\Rightarrow y=-4$

Пересечение с осью $x$:
$\frac{2}{x-1}-4=0\Rightarrow \frac{2}{x-1}=4\Rightarrow 2=4(x-1)\Rightarrow 2=4x-4\Rightarrow 4x=6\Rightarrow x=\frac{3}{2}=1\frac{1}{2}$

Пересечение с осью $y$:
$y=\frac{2}{0-1}-4=-2-4=-6$

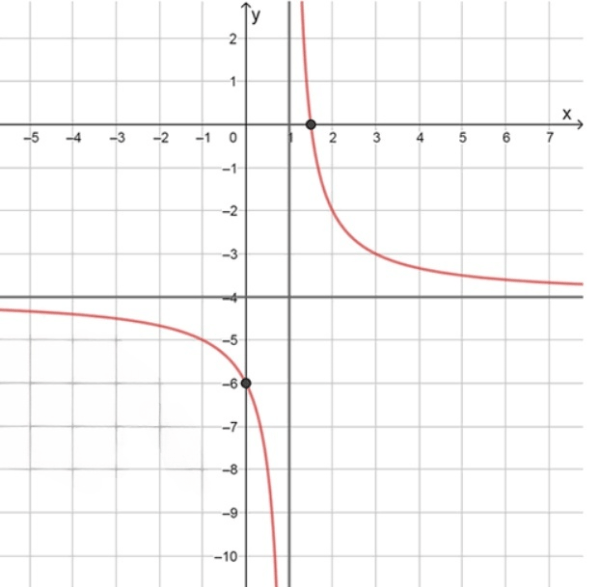
График:

Гипербола с асимптотами $x=1$, $y=-4$, сдвинута на 1 единицу вправо и 4 вниз.
Пересечения: $x=1\frac{1}{2}$, $y=-6$

г) $y=-\frac{6}{x-3}-2$

Вертикальная асимптота:
$x-3=0\Rightarrow x=3$

Горизонтальная асимптота:
$y=-2$

Пересечение с осью $x$:
$-\frac{6}{x-3}-2=0\Rightarrow -\frac{6}{x-3}=2\Rightarrow \frac{6}{x-3}=-2\Rightarrow 6=-2(x-3)\Rightarrow 6$

$=-2x+6\Rightarrow -2x=0\Rightarrow x=0$

Пересечение с осью $y$:
$y=-\frac{6}{0-3}-2=2-2=0$

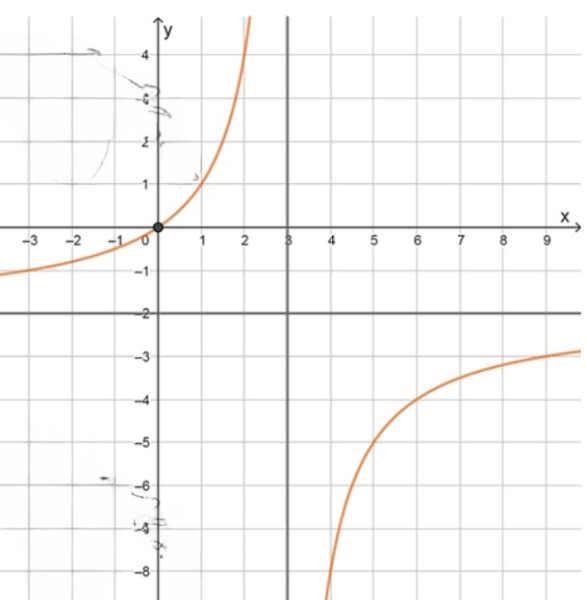
График:

Гипербола, отражённая, сдвинута на 3 вправо и 2 вниз.
Асимптоты: $x=3$, $y=-2$
Пересечения: $x=0$, $y=0$

Ответ:
$\boxed{{\displaystyle \text{Графики построены и описаны выше.}}}$