ГДЗ по Алгебре 9 Класс Номер 318 Дорофеев, Суворова — Подробные Ответы

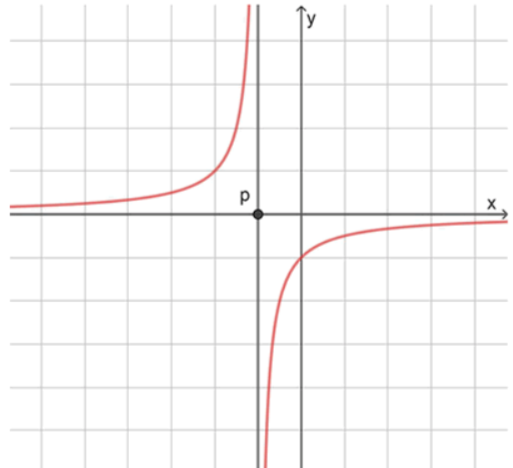
1) Укажите асимптоты графика функции и постройте этот график по точкам:

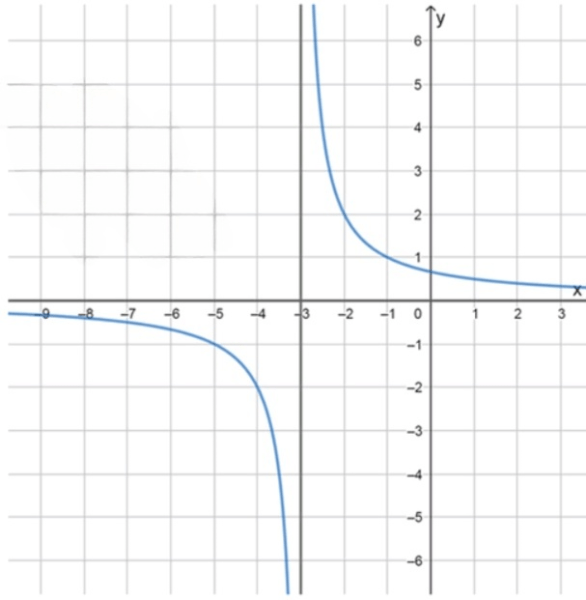
а) $y=\frac{2}{x+3}$;

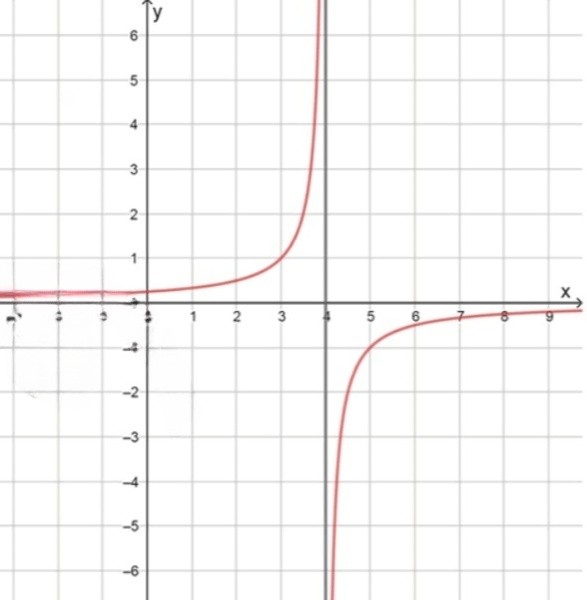
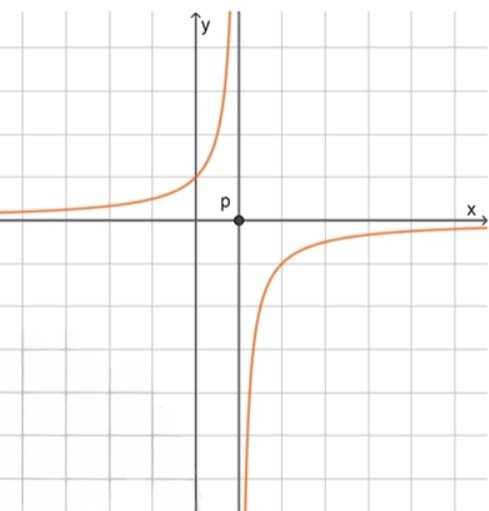
б) $y=-\frac{1}{x-4}$.

2) Покажите с помощью схематического рисунка, как расположена в координатной плоскости гипербола, заданная формулой $y=\frac{k}{x+p}$, если:

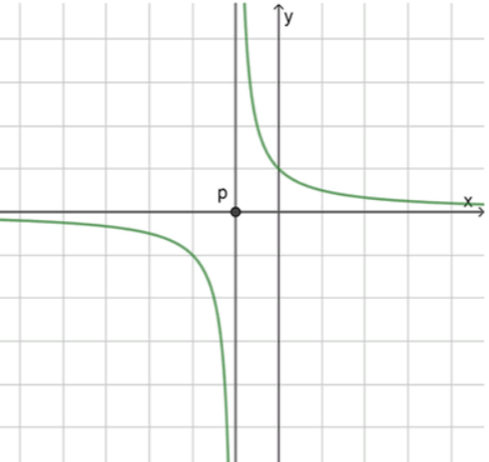
а) $k>0$, $p>0$;

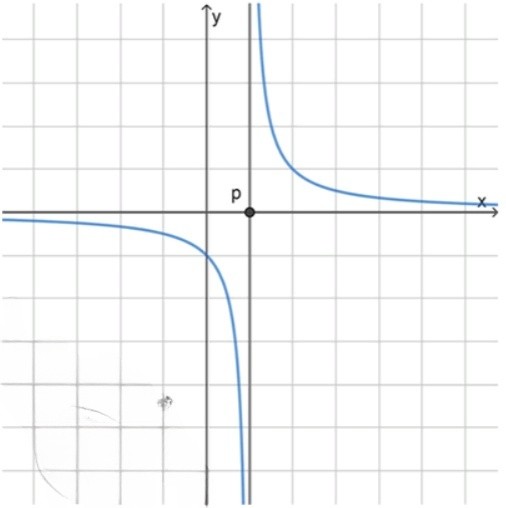
б) $k>0$, $p<0$;

в) $k<0$, $p>0$;

г) $k<0$, $p<0$.

1)

а) $y=\frac{2}{x+3}$:

• вертикальная асимптота: $x=-3$;
• горизонтальная асимптота: $y=0$;

б) $y=$$$$-\frac{1}{x-4}$:

• вертикальная асимптота: $x=4$;
• горизонтальная асимптота: $y=0$;

2) $y=\frac{k}{x+p}$

• вертикальная асимптота: $x=-p$;
• горизонтальная асимптота: $y=0$

а) $k>0$, $p>0$ — гипербола расположена в I и III четвертях, вертикальная асимптота $x=-p$, график смещён влево

б) $k>0$, $p<0$ — гипербола в I и III четвертях, вертикальная асимптота $x=-p$, график смещён вправо

в) $k<0$, $p>0$ — гипербола во II и IV четвертях, вертикальная асимптота $x=-p$, график смещён влево

г) $k<0$, $p<0$ — гипербола во II и IV четвертях, вертикальная асимптота $x=-p$, график смещён вправо

1)

а) $y=\frac{2}{x+3}$

Для функции дробно-рационального вида $y=\frac{2}{x+3}$ необходимо проанализировать её свойства и поведение на различных участках.

Функция определена при всех значениях $x$, кроме тех, при которых знаменатель обращается в ноль. В данном случае $x+3=0$, откуда $x=-3$. Это значение исключается из области определения, и при нём возникает вертикальная асимптота.

Вертикальная асимптота — это прямая, к которой график функции стремится, но не пересекает её. В этом случае:

$x=-3$

Также при стремлении $x\to \mathrm{\infty }$ и $x\to -\mathrm{\infty }$, дробь $\frac{2}{x+3}$ стремится к нулю, потому что числитель остаётся постоянным, а знаменатель растёт по модулю. Это означает, что существует горизонтальная асимптота:

$y=0$

Рассчитаем значения функции в характерных точках по обе стороны от вертикальной асимптоты:

При $x=-7$: $y=\frac{2}{-7+3}=\frac{2}{-4}=-\frac{1}{2}$

При $x=-5$: $y=\frac{2}{-5+3}=\frac{2}{-2}=-1$

При $x=-4$: $y=\frac{2}{-4+3}=\frac{2}{-1}=-2$

При $x=-\mathrm{3,5}$: $y=\frac{2}{-\mathrm{3,5}+3}=\frac{2}{-\mathrm{0,5}}=-4$

При $x=-\mathrm{2,5}$: $y=\frac{2}{-\mathrm{2,5}+3}=\frac{2}{\mathrm{0,5}}=4$

При $x=-2$: $y=\frac{2}{-2+3}=\frac{2}{1}=2$

При $x=-1$: $y=\frac{2}{-1+3}=\frac{2}{2}=1$

При $x=1$: $y=\frac{2}{1+3}=\frac{2}{4}=\frac{1}{2}$

Таким образом, для каждого значения $x$ мы получаем соответствующее значение $y$. Поведение функции симметрично относительно точки перегиба (которой здесь нет), а график представляет собой ветви гиперболы в I и III четвертях, так как $k=2>0$, то есть положительное число.

б) $y=-\frac{1}{x-4}$

Подобный анализ проведём для функции $y=-\frac{1}{x-4}$. В этой функции знаменатель обращается в ноль при $x=4$, значит:

$x=4$ — вертикальная асимптота

При $x\to \mathrm{\infty }$ или $x\to -\mathrm{\infty }$ дробь стремится к нулю, следовательно:

$y=0$ — горизонтальная асимптота

Так как перед дробью стоит минус, то график отражён относительно оси $x$, и ветви гиперболы окажутся во II и IV четвертях. Это типично для функций с отрицательным значением коэффициента $k$.

Рассчитаем значения функции:

При $x=2$: $y=-\frac{1}{2-4}=-\frac{1}{-2}=\frac{1}{2}$

При $x=3$: $y=-\frac{1}{3-4}=-\frac{1}{-1}=1$

При $x=\mathrm{3,5}$: $y=-\frac{1}{\mathrm{3,5}-4}=-\frac{1}{-\mathrm{0,5}}=2$

При $x=\mathrm{4,5}$: $y=-\frac{1}{\mathrm{4,5}-4}=-\frac{1}{\mathrm{0,5}}=-2$

При $x=5$: $y=-\frac{1}{5-4}=-\frac{1}{1}=-1$

При $x=6$: $y=-\frac{1}{6-4}=-\frac{1}{2}$

Таким образом, значения функции положительны при $x<4$ и отрицательны при $x>4$, с разрывом при $x=4$.

$\mathrm{2)\; y}=\frac{k}{x+p}$

Рассмотрим обобщённый вид функции:

$y=\frac{k}{x+p}$

Функция определена при $x\mathrm{\ne }-p$, так как в этой точке знаменатель равен нулю.

Вертикальная асимптота: $x=-p$

При $x\to \mathrm{\infty }$ или $x\to -\mathrm{\infty }$ функция стремится к нулю:

Горизонтальная асимптота: $y=0$

Теперь исследуем, как положение гиперболы зависит от знаков $k$ и $p$.

а) $k>0$, $p>0$

Тогда $x+p=0\Rightarrow x=-p$ — вертикальная асимптота.

Поскольку $k>0$, график представляет собой стандартную гиперболу с ветвями в I и III четвертях, но сдвинутую влево на $p$ единиц. То есть ось симметрии проходит через точку $x=-p$.

б) $k>0$, $p<0$

Асимптота по-прежнему $x=-p$, но теперь $p<0$, следовательно, $-p>0$, и асимптота сдвигается вправо.

График по-прежнему в I и III четвертях, но центр симметрии находится правее, чем в предыдущем случае.

в) $k<0$, $p>0$

Теперь $k<0$, значит, гипербола будет отражена относительно оси $x$. Ветви функции окажутся во II и IV четвертях. Асимптота — $x=-p$, сдвиг влево.

г) $k<0$, $p<0$

Отрицательное $k$ даёт гиперболу в II и IV четвертях. Поскольку $p<0$, то $-p>0$, вертикальная асимптота расположена справа от начала координат, график сдвинут вправо.