
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 317 Дорофеев, Суворова — Подробные Ответы
1) Укажите асимптоты графика функции и постройте этот график по точкам:
а) ;
б) .
2) Покажите с помощью схематического рисунка, как расположена в координатной плоскости гипербола, заданная формулой , если:
а) , ;
б) , ;
в) , ;
г) , .
1)
а) :
- вертикальная асимптота: ;
- горизонтальная асимптота: ;
б) :
- вертикальная асимптота: ;
- горизонтальная асимптота: ;
2)
- вертикальная асимптота: ;
- горизонтальная асимптота: ;
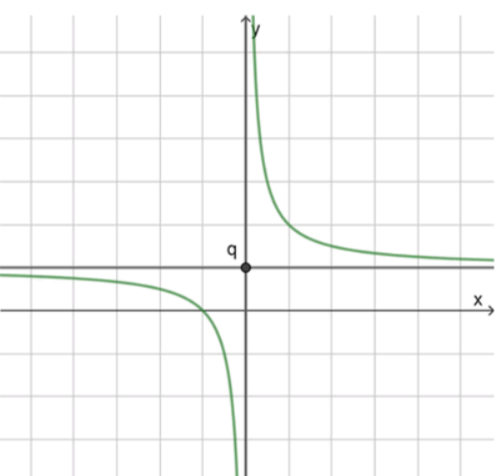
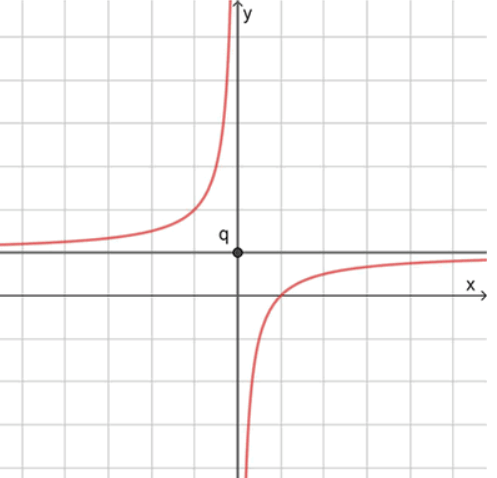
а) , — гипербола в I и III четвертях, смещена вверх на
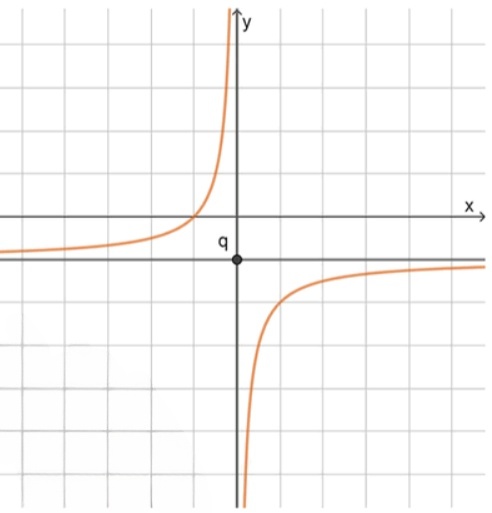
б) , — гипербола во II и IV четвертях, смещена вверх на
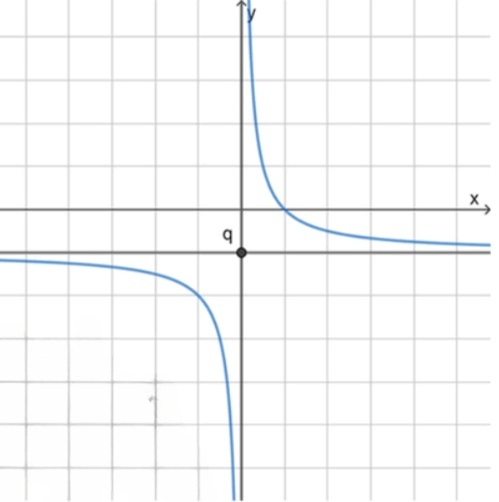
г) , — гипербола во II и IV четвертях, смещена вниз на
|q|
1)
а)
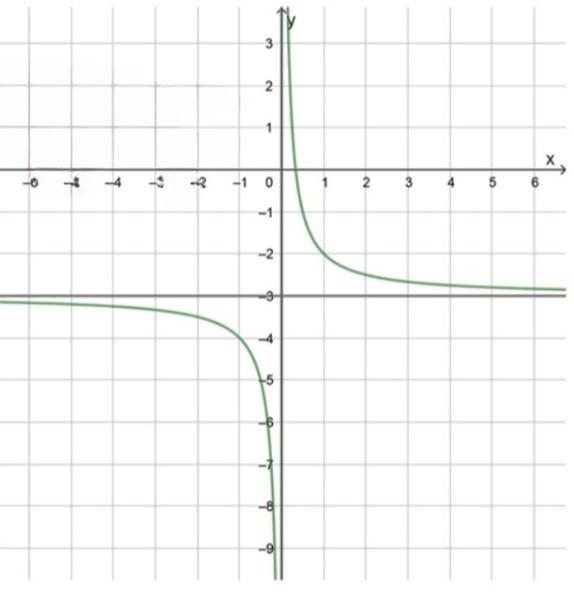
Функция задана как гипербола, сдвинутая на 3 единицы вниз. Основной вид гиперболы — . При вычитании числа 3 из всей функции происходит вертикальный сдвиг графика вниз на 3 единицы. Таким образом, горизонтальная асимптота перемещается с прямой на прямую , а вертикальная асимптота остаётся без изменений — это прямая , поскольку деление на ноль невозможно и функция не определена при
График разбит на две ветви:
для , значения функции положительные и стремятся к бесконечности при , а при стремятся к ;
для , значения функции отрицательные, стремятся к минус бесконечности при , и также стремятся к при
Таблица значений:
Асимптоты:
вертикальная ,
горизонтальная
б)
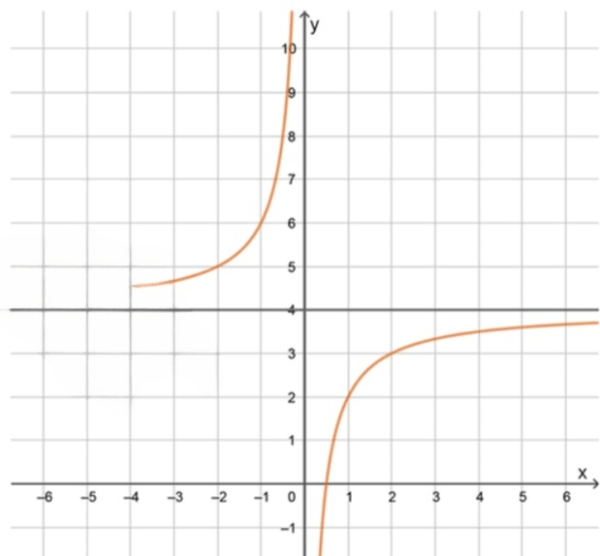
Функция получена из базовой гиперболы , умножением на , что отражает график относительно оси Ox и растягивает его в 2 раза по оси Oy, а затем сдвигом на 4 единицы вверх. Таким образом:
Вертикальная асимптота остаётся прежней — , так как знаменатель не может быть равен нулю.
Горизонтальная асимптота теперь находится на уровне , так как именно к этому значению стремится функция при
Для положительных :
Для отрицательных :
Таблица значений:
Асимптоты:
вертикальная ,
горизонтальная
в)
Это обобщённая формула гиперболы, где:
- отвечает за направление ветвей (знаки и их положение),
- — вертикальное смещение графика (на сколько единиц вверх или вниз относительно оси Ox),
- вертикальная асимптота всегда , так как при функция не определена,
- горизонтальная асимптота — , так как при , дробная часть стремится к нулю, а значение функции к
а) если , :
ветви гиперболы располагаются в I и III координатных четвертях, горизонтальная асимптота — , вертикальная —
б) если , :
ветви гиперболы располагаются во II и IV координатных четвертях, асимптоты те же
в) если , :
ветви гиперболы в I и III четвертях, график сдвинут вниз, асимптоты: ,
г) если , :
ветви во II и IV четвертях, сдвиг вниз, асимптоты: ,




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!