ГДЗ по Алгебре 9 Класс Номер 315 Дорофеев, Суворова — Подробные Ответы

Докажите двумя способами, что при всех значениях переменной $a$ верно неравенство:

а) $a^2 + a + 1 > 0$;

б) $-a^2 + 3x — 5 < 0$.

Указания:

1) Используйте графические соображения.

2) Выделите квадрат двучлена и сравните полученное выражение с нулем.

а) $a^2 + a + 1 > 0$:

1) Первый способ:

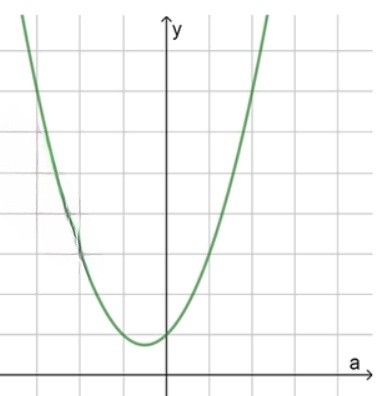
Ветви параболы направлены вверх;

Вершина находится в точке с координатами:
$a = -\frac{1}{2} = -0{,}5 \quad \text{и} \quad y = (-0{,}5)^2 — 0{,}5 + 1 = 0{,}25 + 0{,}5 = 0{,}75$;

Схематический рисунок:

Следовательно, $a^2 + a + 1 > 0$ при любых значениях $a$

2) Второй способ:
$a^2 + a + 1 = a^2 + 2 \cdot \frac{1}{2}a + \frac{1}{4} + \frac{3}{4} = \left(a + \frac{1}{2}\right)^2 + \frac{3}{4} > 0$

Следовательно, $a^2 + a + 1 > 0$ при любых значениях $a$

б) $-a^2 + 3a — 5 < 0$:

1) Первый способ:

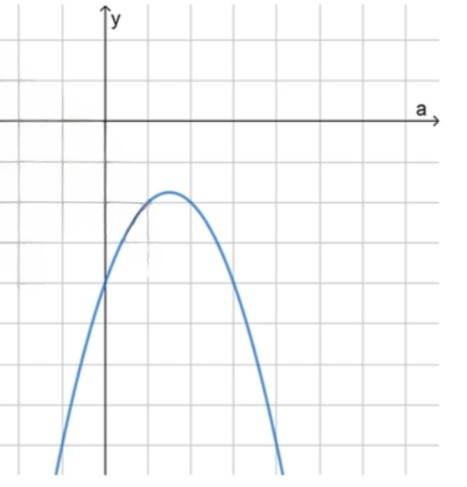
Ветви параболы направлены вниз;

Вершина находится в точке с координатами:
$a = -\frac{3}{-2} = 1{,}5 \quad \text{и} \quad y = -(1{,}5)^2 + 3 \cdot 1{,}5 — 5 = -2{,}25 + 4{,}5 — 5 = -2{,}75$;

Схематический рисунок:

Следовательно, $-a^2 + 3a — 5 < 0$ при любых значениях $a$

2) Второй способ:
$-a^2 + 3a — 5 = -a^2 + 2 \cdot 1{,}5a — 2{,}25 — 2{,}75 = -(a — 1{,}5)^2 — 2{,}75 < 0$

Следовательно, $-a^2 + 3a — 5 < 0$ при любых значениях $a$

а) $a^2 + a + 1 > 0$

1 способ: графический
Функция $y = a^2 + a + 1$ является квадратичной функцией. Коэффициент при $a^2$ равен $1 > 0$, значит ветви параболы направлены вверх. Вершина параболы находится в точке с абсциссой $a = -\frac{1}{2}$, подставим это значение в выражение:

$y = \left(-\frac{1}{2}\right)^2 + \left(-\frac{1}{2}\right) + 1 = \frac{1}{4} — \frac{1}{2} + 1 = \frac{3}{4}$

Вершина параболы соответствует наименьшему значению функции, и оно положительно: $\frac{3}{4} > 0$. Поскольку парабола направлена вверх, то значение функции положительно при любом значении $a$

Следовательно, при любых значениях $a$ выполняется неравенство $a^2 + a + 1 > 0$

2 способ: выделение полного квадрата
Преобразуем выражение:

$a^2 + a + 1 = a^2 + 2 \cdot \frac{1}{2}a + \frac{1}{4} + \frac{3}{4} = \left(a + \frac{1}{2}\right)^2 + \frac{3}{4}$

Выражение представляет собой сумму квадрата и положительного числа. Поскольку $\left(a + \frac{1}{2}\right)^2 \geq 0$ и $\frac{3}{4} > 0$, то всё выражение строго больше нуля:

$\left(a + \frac{1}{2}\right)^2 + \frac{3}{4} > 0$

Значит, $a^2 + a + 1 > 0$ при всех $a$

б) $-a^2 + 3a — 5 < 0$

1 способ: графический
Функция $y = -a^2 + 3a — 5$ также является квадратной. Коэффициент при $a^2$ отрицателен: $-1 < 0$, значит ветви параболы направлены вниз. Вершина параболы находится при $a = -\frac{3}{2 \cdot (-1)} = \frac{3}{2}$, найдём значение функции в этой точке:

$y = -\left(\frac{3}{2}\right)^2 + 3 \cdot \frac{3}{2} — 5 = -\frac{9}{4} + \frac{9}{2} — 5 = -\frac{9}{4} + \frac{18}{4} — \frac{20}{4} = -\frac{11}{4}$

Наибольшее значение функции равно $-\frac{11}{4}$, что меньше нуля. Так как это наибольшее значение, то при всех остальных значениях функция также меньше нуля.

Следовательно, при любом $a$ выполняется неравенство $-a^2 + 3a — 5 < 0$

2 способ: выделение полного квадрата
Преобразуем выражение:

$-a^2 + 3a — 5 = -(a^2 — 3a + 5) = -\left(a^2 — 2 \cdot \frac{3}{2}a + \frac{9}{4} — \frac{9}{4} + 5\right) = -\left( \left(a — \frac{3}{2} \right)^2 — \frac{9}{4} + 5 \right)$

$= -\left( \left(a — \frac{3}{2} \right)^2 + \frac{11}{4} \right)$

Квадрат любого выражения неотрицателен, а $\frac{11}{4} > 0$, значит выражение $\left(a — \frac{3}{2} \right)^2 + \frac{11}{4} > 0$, а значит:

$-\left( \left(a — \frac{3}{2} \right)^2 + \frac{11}{4} \right) < 0$

Следовательно, при всех значениях $a$ выполняется неравенство $-a^2 + 3a — 5 < 0$