ГДЗ по Алгебре 9 Класс Номер 314 Дорофеев, Суворова — Подробные Ответы

Найдите все целые значения $t$, при которых уравнение $4tx^2 + 5x + m = 0$ имеет два корня.

б) $4mx^2 + 5x + m = 0$:

1) Уравнение имеет два корня при $D > 0$:
$(5 — 4m)(5 + 4m) > 0$

$a = -16 < 0$, значит ветви направлены вниз;

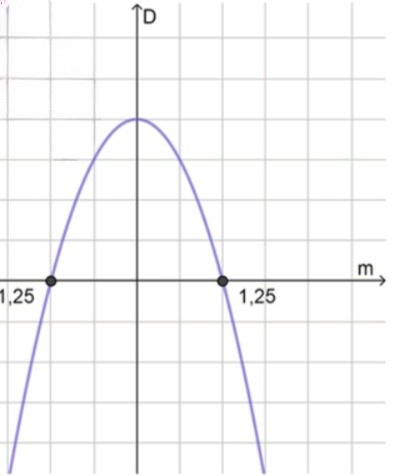
3) Нули функции:
$5 — 4m_1 = 0, \text{ отсюда } m_1 = \frac{-5}{-4} = 1{,}25;$
$5 + 4m_2 = 0, \text{ отсюда } m_2 = \frac{5}{4} = -1{,}25;$

4) Схематический рисунок:

$-1{,}25 < m < 1{,}25$

5) Но при $a = 0$ получим линейное уравнение $5x = 0$, которое имеет только один корень, значит:
$m \in (-1; 0) \cup (0; 1)$

6) Целые значения: $m = -1$ и $1$

$4mx^2 + 5x + m = 0$

Это квадратное уравнение, в котором переменным параметром является коэффициент $m$. Чтобы уравнение имело два корня, необходимо, чтобы дискриминант был строго положительным:

$D = 5^2 — 4 \cdot 4m \cdot m = 25 — 16m^2$

Рассмотрим неравенство:
$25 — 16m^2 > 0$

Переносим $16m^2$ вправо:
$25 > 16m^2$

Делим обе части на 16:
$\frac{25}{16} > m^2$

Это неравенство квадратов:
$m^2 < \frac{25}{16}$

Извлекаем корень:
$|m| < \frac{5}{4} \Rightarrow -\frac{5}{4} < m < \frac{5}{4}$

Это означает, что параметр $m$ должен принадлежать открытому интервалу от $-1{,}25$ до $1{,}25$

Однако при $m = 0$, уравнение принимает вид:
$5x + 0 = 0 \Rightarrow x = 0$, что является линейным уравнением и имеет один корень

Следовательно, значение $m = 0$ необходимо исключить из промежутка

Таким образом, окончательный допустимый интервал:
$m \in (-\frac{5}{4}; 0) \cup (0; \frac{5}{4})$

Из этого промежутка находим все целые значения параметра $m$. Это такие $m$, которые удовлетворяют:
$-1{,}25 < m < 0$ или $0 < m < 1{,}25$

Целые значения $m$, лежащие в этих интервалах:
$m = -1$, $m = 1$

Ответ: $m = -1; \, 1$