ГДЗ по Алгебре 9 Класс Номер 310 Дорофеев, Суворова — Подробные Ответы

При каких значениях $b$ уравнение $x^2 + bx + 4 = 0$ имеет два корня? Имеет ли уравнение корни при $b = -25.5$; $1.5$; $5.36$?

а) $x^2 + bx + 4 = 0$:

$D = b^2 — 4 \cdot 4 = b^2 — 16 = (b — 4)(b + 4);$

1) Уравнение имеет два корня при $D > 0$:
$(b-4)(b+4)>0;$

2) a = 1 > 0, значит ветви направлены вверх;$(b — 4)(b + 4) > 0;$

3) Нули функции:
$b_1 — 4 = 0, \text{ отсюда } b_1 = 4;$
$b_2 + 4 = 0, \text{ отсюда } b_2 = -4;$

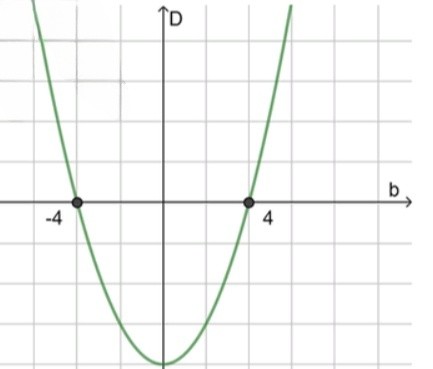
4) Схематический рисунок:

$b \in (-\infty; -4) \cup (4; +\infty);$

Имеет корни при:
$b = -25.5; \, 5.36;$

Не имеет корней при:
$b = 1.5;$

б) $-2x^2 — bx — 8 = 0$:

$D = b^2 — 4 \cdot (-2) \cdot (-8) = b^2 — 64 = (b — 8)(b + 8);$

1) Уравнение имеет хотя бы один корень при $D \geq 0$:
$(b-8)(b+8)\ge 0;$

2) a = 1 > 0, значит ветви направлены вверх;$2) a = 1 > 0, значит ветви направлены вверх;$$2) a = 1 > 0, значит ветви направлены вверх;(b — 8)(b + 8) \geq 0;$

3) Нули функции:
$b_1 — 8 = 0, \text{ отсюда } b_1 = 8;$
$b_1 + 8 = 0, \text{ отсюда } b_1 = -8;$

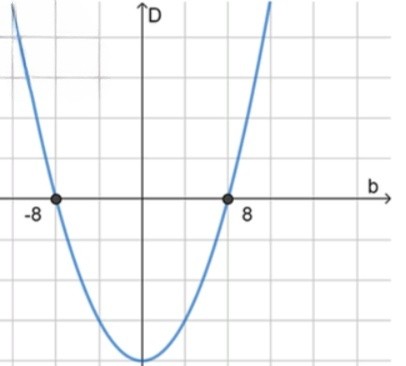
4) Схематический рисунок:

$b \in (-\infty; -8] \cup [8; +\infty);$

Отрицательное значение:
$b = -12; \, -10; \, -8;$

а) $x^2 + bx + 4 = 0$

Это квадратное уравнение вида $ax^2 + bx + c = 0$, где $a = 1$, $b$ — параметр, $c = 4$. Чтобы выяснить, при каких значениях $b$ уравнение имеет два корня, необходимо воспользоваться дискриминантом.

Формула дискриминанта:
$D = b^2 — 4ac$

Подставляем значения:
$D = b^2 — 4 \cdot 1 \cdot 4 = b^2 — 16$

Рассматриваем случай двух корней — это происходит при $D > 0$:

$b^2 — 16 > 0$

Решим это неравенство:
$b^2 > 16 \Rightarrow |b| > 4$

Отсюда следует:
$b < -4$ или $b > 4$

Ответ: $b \in (-\infty; -4) \cup (4; +\infty)$

Проверка заданных значений:

$b = -25.5 \Rightarrow -25.5 < -4 \Rightarrow$ входит в область — два корня есть
$b = 1.5 \Rightarrow -4 < 1.5 < 4 \Rightarrow$ не входит — корней нет
$b = 5.36 \Rightarrow 5.36 > 4 \Rightarrow$ входит — два корня есть

б) $-2x^2 — bx — 8 = 0$

Это квадратное уравнение, в котором коэффициенты:
$a = -2$, $b$ — параметр, $c = -8$

Чтобы определить, при каких значениях $b$ уравнение имеет хотя бы один корень, находим дискриминант по формуле:

$D = b^2 — 4ac$

Подставим $a$ и $c$:

$D = b^2 — 4 \cdot (-2) \cdot (-8) = b^2 — 64$

Чтобы уравнение имело два корня — нужно $D > 0$,
чтобы имело один корень — нужно $D = 0$,
чтобы не имело корней — $D < 0$

Требуется, чтобы был хотя бы один корень, т.е. $D \geq 0$

Решим неравенство:

$b^2 — 64 \geq 0$

$b^2 \geq 64 \Rightarrow |b| \geq 8$

Тогда:

$b \leq -8$ или $b \geq 8$

Ответ: $b \in (-\infty; -8] \cup [8; +\infty)$