ГДЗ по Алгебре 9 Класс Номер 31 Дорофеев, Суворова — Подробные Ответы

Постройте график функции

$y=\frac{\sqrt{2}}{x}$.

а) Проходит ли график этой функции хотя бы через одну точку, обе координаты которой — рациональные числа?

б) Найдите координаты точек графика, у которых абсцисса и ордината равны.

$y=\frac{\sqrt{2}}{x}$;

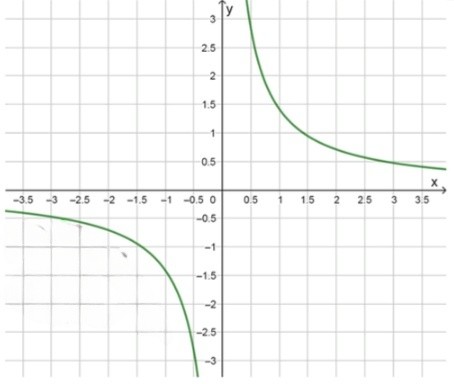
График функции — гипербола в I и III четвертях:

а) Если $x$ и $y$ — рациональные числа, тогда:
$y=\frac{\sqrt{2}}{x}$, отсюда $xy=\sqrt{2}$;
$\sqrt{2}$ — иррациональное число, что неверно, значит данный график не проходит ни через одну из таких точек;

б) Если $x=y$, тогда:
$y=\frac{\sqrt{2}}{y}\Rightarrow y^2=\sqrt{2}$, отсюда $x=y=\pm \sqrt[4]{2}$;
Ответ: $(\sqrt[4]{2};\sqrt[4]{2})$ и $(-\sqrt[4]{2};-\sqrt[4]{2})$.

Рассмотрим функцию:

$$y=\frac{\sqrt{2}}{x}$$

Эта функция задает гиперболу, которая проходит через I и III четверти, так как при положительном $x$ значение $y$ также положительно, а при отрицательном $x$ значение $y$ отрицательно. Важно отметить, что график функции не пересекает оси $x$ и $y$, так как для этих точек выражение $\frac{\sqrt{2}}{x}$ не определено (когда $x=0$, выражение будет бесконечным).

Из таблицы значений мы видим несколько точек, через которые проходит график функции:

Теперь проверим, могут ли все эти значения быть рациональными числами.

а) Допустим, что и $x$, и $y$ — рациональные числа. Тогда из формулы функции $y=\frac{\sqrt{2}}{x}$ получаем:

$$xy=\sqrt{2}$$

Однако, $\sqrt{2}$ является иррациональным числом, а произведение двух рациональных чисел всегда рационально. Это приводит к противоречию, так как мы не можем получить иррациональное число, если оба множителя рациональны. Таким образом, график функции не проходит через точки, где обе координаты являются рациональными числами.

б) Теперь рассмотрим случай, когда $x=y$. Тогда из формулы функции $y=\frac{\sqrt{2}}{x}$ получаем:

$$y=\frac{\sqrt{2}}{y}$$

Умножим обе части этого уравнения на $y$, чтобы избавиться от дроби:

$$y^2=\sqrt{2}$$

Теперь извлекаем квадратный корень из обеих сторон:

$$y=\pm \sqrt[4]{2}$$

Поскольку $x=y$, то $x$ также равно $\pm \sqrt[4]{2}$. Следовательно, координаты точек, где абсцисса и ордината равны, будут:

$$(\sqrt[4]{2},\sqrt[4]{2})\text{и}(-\sqrt[4]{2},-\sqrt[4]{2})$$

Таким образом, график функции проходит через две точки, где абсцисса и ордината равны: $(\sqrt[4]{2},\sqrt[4]{2})$ и $(-\sqrt[4]{2},-\sqrt[4]{2})$.