ГДЗ по Алгебре 9 Класс Номер 308 Дорофеев, Суворова — Подробные Ответы

Найдите допустимые значения переменной в выражении:

а) $\sqrt{7x^2 + 6x — 1}$;

б) $\sqrt{4 + x — 0.5x^2}$;

в) $\sqrt{\frac{x^2}{8} + \frac{x}{4} — 1}$;

г) $\sqrt{3 — \frac{1}{2}x^2}$.

а) $\sqrt{7x^2 + 6x — 1}$:

Имеет смысл при: $7x^2 + 6x — 1 \geq 0$;

$a = 7 > 0$, значит ветви направлены вверх;

2) Нули функции:

$7x^2 + 6x — 1 = 0;$

$D = 6^2 + 4 \cdot 7 = 36 + 28 = 64, \text{тогда:}$

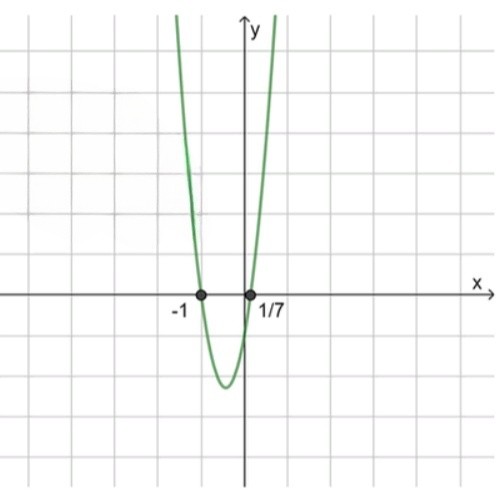
$x_1 = \frac{-6 — 8}{2 \cdot 7} = -1 \quad \text{и} \quad x_2 = \frac{-6 + 8}{2 \cdot 7} = \frac{1}{7};$

3) Схематический рисунок:

Ответ: $(-\infty; -1] \cup \left[ \frac{1}{7}; +\infty \right)$.

б) $\sqrt{4 + x — 0.5x^2}$:

Имеет смысл при: $4 + x — 0.5x^2 \geq 0$;

$a = -0.5 < 0$, значит ветви направлены вниз;

2) Нули функции:

$-0.5x^2 + x + 4 = 0;$

$D = 1 + 4 \cdot 0.5 \cdot 4 = 1 + 8 = 9, \text{тогда:}$

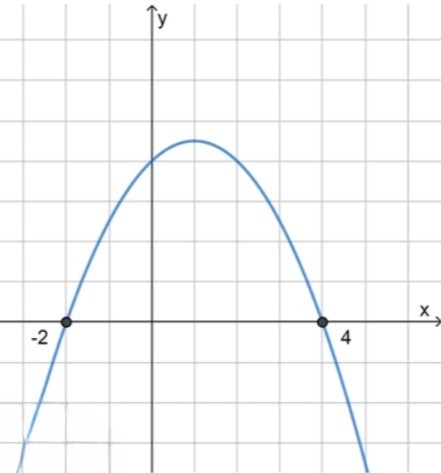
$x_1 = \frac{-1 — 3}{2 \cdot (-0.5)} = 4 \quad \text{и} \quad x_2 = \frac{-1 + 3}{2 \cdot (-0.5)} = -2;$

3) Схематический рисунок:

Ответ: $[-2; 4]$.

г) $\sqrt{3 — \frac{1}{2}x^2}$:

Имеет смысл при: $3 — \frac{1}{2}x^2 \geq 0$;

$a = -\frac{1}{2} < 0$, значит ветви направлены вниз;

2) Нули функции:

$3 — \frac{1}{2}x^2 = 0;$

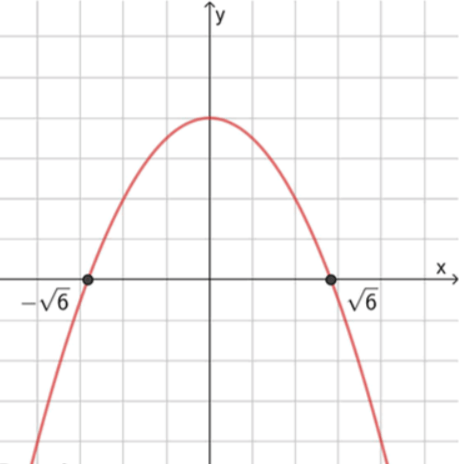
$-\frac{1}{2}x^2 = -3 \quad \Rightarrow \quad x^2 = 6, \text{отсюда } x = \pm \sqrt{6};$

3) Схематический рисунок:

Ответ: $[-\sqrt{6}; \sqrt{6}]$.

а) $\sqrt{7x^2 + 6x — 1}$:

$7x^2 + 6x — 1 \geq 0$

$a = 7 > 0$, парабола ветвями вверх

$7x^2 + 6x — 1 = 0$

$D = 6^2 — 4 \cdot 7 \cdot (-1) = 36 + 28 = 64$

$x_1 = \frac{-6 — 8}{2 \cdot 7} = \frac{-14}{14} = -1$

$x_2 = \frac{-6 + 8}{2 \cdot 7} = \frac{2}{14} = \frac{1}{7}$

Парабола выше оси Ox вне интервалов между корнями: $x \leq -1$ или $x \geq \frac{1}{7}$

Ответ: $(-\infty; -1] \cup \left[ \frac{1}{7}; +\infty \right)$

б) $\sqrt{4 + x — 0.5x^2}$:

$4 + x — 0.5x^2 \geq 0$

Приведём к стандартному виду: $-0.5x^2 + x + 4 \geq 0$

$a = -0.5 < 0$, парабола ветвями вниз

$-0.5x^2 + x + 4 = 0$

$D = 1^2 — 4 \cdot (-0.5) \cdot 4 = 1 + 8 = 9$

$x_1 = \frac{-1 — 3}{2 \cdot (-0.5)} = \frac{-4}{-1} = 4$

$x_2 = \frac{-1 + 3}{2 \cdot (-0.5)} = \frac{2}{-1} = -2$

Так как ветви вниз, выражение неотрицательно между корнями: $-2 \leq x \leq 4$

Ответ: $[-2; 4]$

г) $\sqrt{3 — \frac{1}{2}x^2}$:

$3 — \frac{1}{2}x^2 \geq 0$

Переносим: $-\frac{1}{2}x^2 + 3 \geq 0$

$a = -\frac{1}{2} < 0$, ветви вниз

$-\frac{1}{2}x^2 + 3 = 0$

$-\frac{1}{2}x^2 = -3$

$x^2 = 6$

$x = \pm \sqrt{6}$

Функция неотрицательна между корнями: $-\sqrt{6} \leq x \leq \sqrt{6}$

Ответ: $[-\sqrt{6}; \sqrt{6}]$