ГДЗ по Алгебре 9 Класс Номер 306 Дорофеев, Суворова — Подробные Ответы

а) Найдите решения неравенства $5x^2 \geq 4x + 1$, принадлежащие промежутку $[-2; 2]$.

б) Найдите решения неравенства $5x — 1 > 4x^2$, принадлежащие промежутку $\left[ \frac{1}{3}; \frac{3}{2} \right]$.

а) $5x^2 \geq 4x + 1, \quad x \in [-2; 2]$:
$5x^2 — 4x — 1 \geq 0;$

$a = 5 > 0$, значит ветви направлены вверх;

2) Нули функции:
$5x^2 — 4x — 1 = 0;$
$D = 4^2 + 4 \cdot 5 = 16 + 20 = 36, \text{тогда:}$
$x_1 = \frac{4 — 6}{2 \cdot 5} = -0.2 \quad \text{и} \quad x_2 = \frac{4 + 6}{2 \cdot 5} = 1;$

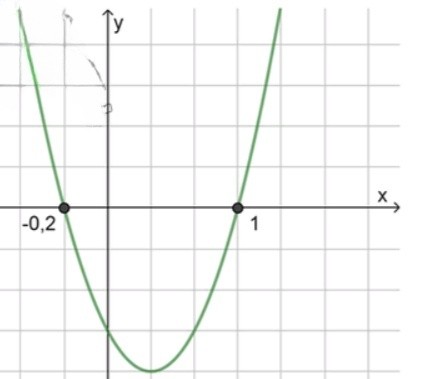
3) Схематический рисунок:

$(-\infty; -0.2] \cup [1; +\infty);$

4) Решения на указанном промежутке:
$x \in [-2; -0.2] \cup [1; 2];$

Ответ: $[-2; -0.2] \cup [1; 2]$.

б) $5x — 1 > 4x^2, \quad x \in \left[ \frac{1}{3}; \frac{3}{2} \right]$:
$-4x^2 + 5x — 1 > 0;$

$a = -4 < 0$, значит ветви направлены вниз;

2) Нули функции:
$-4x^2 + 5x — 1 = 0;$
$D = 5^2 — 4 \cdot 4 = 25 — 16 = 9, \text{тогда:}$
$x_1 = \frac{-5 — 3}{2 \cdot (-4)} = 1 \quad \text{и} \quad x_2 = \frac{-5 + 3}{2 \cdot (-4)} = \frac{1}{4};$

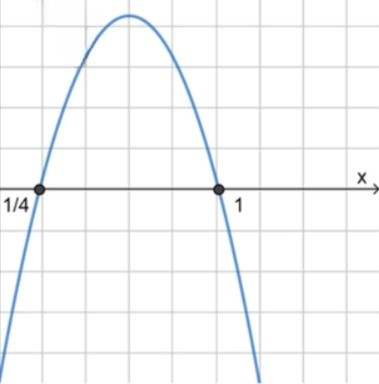
3) Схематический рисунок:

$\frac{1}{4} < x < 1;$

4) Решения на указанном промежутке:
$x \in \left[ \frac{1}{3}; 1 \right);$

Ответ: $\left[ \frac{1}{3}; 1 \right)$.

а) $5x^2 \geq 4x + 1, \quad x \in [-2; 2]$
Переносим все слагаемые в одну часть:
$5x^2 — 4x — 1 \geq 0$
Это квадратное неравенство. Рассмотрим квадратный трёхчлен $f(x) = 5x^2 — 4x — 1$.
Коэффициент при $x^2$ положителен: $a = 5 > 0$, значит ветви параболы направлены вверх.
Найдём корни уравнения $5x^2 — 4x — 1 = 0$:
Вычислим дискриминант:
$D = (-4)^2 — 4 \cdot 5 \cdot (-1) = 16 + 20 = 36$
Найдём корни по формуле:
$x = \frac{-(-4) \pm \sqrt{36}}{2 \cdot 5} = \frac{4 \pm 6}{10}$
$x_1 = \frac{4 — 6}{10} = \frac{-2}{10} = -0.2$
$x_2 = \frac{4 + 6}{10} = \frac{10}{10} = 1$
Парабола принимает значения больше или равные нулю вне интервала между корнями, то есть:
$x \in (-\infty; -0.2] \cup [1; +\infty)$
Теперь пересекаем это множество с отрезком $[-2; 2]$
$[-2; 2] \cap ((-\infty; -0.2] \cup [1; +\infty)) = [-2; -0.2] \cup [1; 2]$

Ответ: $[-2; -0.2] \cup [1; 2]$

б) $5x — 1 > 4x^2, \quad x \in \left[ \frac{1}{3}; \frac{3}{2} \right]$
Переносим всё в одну часть:
$-4x^2 + 5x — 1 > 0$
Рассмотрим квадратный трёхчлен $f(x) = -4x^2 + 5x — 1$.
$a = -4 < 0$, значит ветви параболы направлены вниз.
Найдём корни уравнения $-4x^2 + 5x — 1 = 0$
Вычислим дискриминант:
$D = 5^2 — 4 \cdot (-4) \cdot (-1) = 25 — 16 = 9$
Найдём корни по формуле:
$x = \frac{-5 \pm \sqrt{9}}{2 \cdot (-4)} = \frac{-5 \pm 3}{-8}$
$x_1 = \frac{-5 + 3}{-8} = \frac{-2}{-8} = \frac{1}{4}$
$x_2 = \frac{-5 — 3}{-8} = \frac{-8}{-8} = 1$
Поскольку ветви вниз, неравенство $> 0$ выполняется на интервале между корнями:
$x \in \left( \frac{1}{4}; 1 \right)$
Теперь пересекаем с заданным промежутком $\left[ \frac{1}{3}; \frac{3}{2} \right]$
$\left( \frac{1}{4}; 1 \right) \cap \left[ \frac{1}{3}; \frac{3}{2} \right] = \left[ \frac{1}{3}; 1 \right)$

Ответ: $\left[ \frac{1}{3}; 1 \right)$