ГДЗ по Алгебре 9 Класс Номер 303 Дорофеев, Суворова — Подробные Ответы

Найдите значения $x$, при которых:

а) значения функции $y=3x^2+2x-1$ меньше значений функции $y=x^2-x+1$

б) значения функции $y=-4x^2+x+1$ больше значений функции $y=2-4x$

а) $3x^2+2x-1<x^2-x+1$:

$$3x^2+2x-1-x^2+x-1<0;$$

$$2x^2+3x-2<0;$$

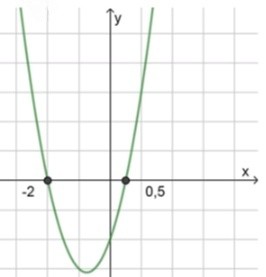
$\mathrm{1)\; a}=2>0$, значит ветви направлены вверх;

2) Нули функции:

$$2x^2+3x-2=0;$$

$$D=3^2+4\cdot 2\cdot 2=9+16=25,\text{тогда:}$$

$$x_1=\frac{-3-5}{2\cdot 2}=-2\text{и}{x}_2=\frac{-3+5}{2\cdot 2}=0.5;$$

3) Схематический рисунок:

Ответ: $(-2;0.5)$.

б) $-4x^2+x+1>2-4x$:

$$-4x^2+x+1-2+4x>0;$$

$$-4x^2+5x-1>0;$$

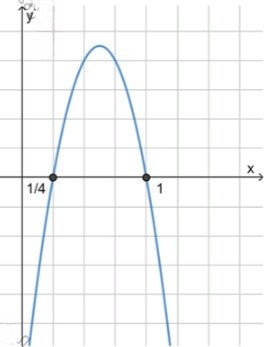
$\mathrm{1)\; a}=-4<0$, значит ветви направлены вниз;

2) Нули функции:

$$-4x^2+5x-1=0;$$

$$D=5^2-4\cdot 4=25-16=9,\text{тогда:}$$

$$x_1=\frac{-5-3}{2\cdot (-4)}=1\text{и}{x}_2=\frac{-5+3}{2\cdot (-4)}=\frac{1}{4};$$

3) Схематический рисунок:

Ответ: $(\frac{1}{4};1)$.

а) $3x^2+2x-1<x^2-x+1$:

$$3x^2+2x-1-x^2+x-1<0;$$

Приведем подобные выражения:

$$(3x^2-x^2)+(2x+x)+(-1-1)<0;$$$$2x^2+3x-2<0;$$

Это неравенство представляет собой квадратичную функцию, и чтобы определить, где она меньше нуля, нам нужно сначала найти ее корни. Рассмотрим дискриминант для уравнения:

$$D=b^2-4ac=3^2-4\cdot 2\cdot (-2)=9+16=25;$$

Так как дискриминант положительный, у нас два корня:

$$x_1=\frac{-b-\sqrt{D}}{2a}=\frac{-3-\sqrt{25}}{2\cdot 2}=\frac{-3-5}{4}=-2;$$

$$$$$$x_2=\frac{-b+\sqrt{D}}{2a}=\frac{-3+\sqrt{25}}{2\cdot 2}=\frac{-3+5}{4}=0.5;$$

Теперь, чтобы решить неравенство $2x^2+3x-2<0$, мы анализируем знаки квадратичной функции на интервалах, определенных этими корнями: $(-\mathrm{\infty },-2)$, $(-2,0.5)$ и $(0.5,+\mathrm{\infty })$.

• Для $x=-3$ (интервал $(-\mathrm{\infty },-2)$):

$$2(-3{)}^2+3(-3)-2=18-9-2=7>0.$$

• Для $x=0$ (интервал $(-2,0.5)$):

$$2(0{)}^2+3(0)-2=-2<0.$$

• Для $x=1$ (интервал $(0.5,+\mathrm{\infty })$):

$$2(1{)}^2+3(1)-2=2+3-2=3>0.$$

Следовательно, неравенство выполняется на интервале $(-2,0.5)$.

Ответ: $(-2;0.5)$.

б) $-4x^2+x+1>2-4x$:

$$-4x^2+x+1-2+4x>0;$$

Приведем подобные выражения:

$$-4x^2+(x+4x)+(1-2)>0;$$

$$$$$$-4x^2+5x-1>0;$$

Для решения этого неравенства сначала находим дискриминант для уравнения $-4x^2+5x-1=0$:

$$D=b^2-4ac=5^2-4\cdot (-4)\cdot (-1)=25-16=9;$$

Положительный дискриминант указывает на наличие двух корней:

$$x_1=\frac{-5-\sqrt{9}}{2\cdot (-4)}=\frac{-5-3}{-8}=\frac{-8}{-8}=1;$$

$$$$$$x_2=\frac{-5+\sqrt{9}}{2\cdot (-4)}=\frac{-5+3}{-8}=\frac{-2}{-8}=\frac{1}{4};$$

Теперь рассмотрим знаки функции $-4x^2+5x-1$ на интервалах $(-\mathrm{\infty },\frac{1}{4})$, $(\frac{1}{4},1)$ и $(1,+\mathrm{\infty })$.

• Для $x=-1$ (интервал $(-\mathrm{\infty },\frac{1}{4})$):

$$-4(-1{)}^2+5(-1)-1=-4-5-1=-10<0.$$

• Для $x=0$ (интервал $(\frac{1}{4},1)$):

$$-4(0{)}^2+5(0)-1=-1<0.$$

• Для $x=2$ (интервал $(1,+\mathrm{\infty })$):

$$-4(2{)}^2+5(2)-1=-16+10-1=-7<0.$$

Так как функция отрицательна на всех интервалах, это означает, что неравенство $-4x^2+5x-1>0$ не имеет решения.

Ответ: $(\frac{1}{4};1)$.