
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 299 Дорофеев, Суворова — Подробные Ответы
а) ;
б) ;
в) ;
г) .
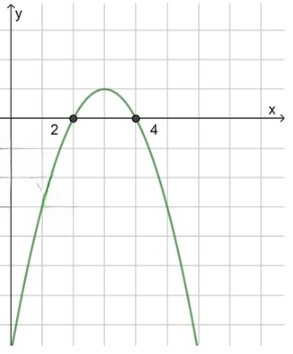
а) :
;
, значит ветви направлены вниз;
2) Нули функции:
, отсюда ;
, отсюда ;
3) Схематический рисунок:
Ответ: .
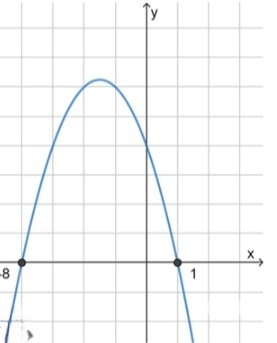
б) :
;
, значит ветви направлены вниз;
2) Нули функции:
, отсюда ;
, отсюда ;
3) Схематический рисунок:
Ответ: .
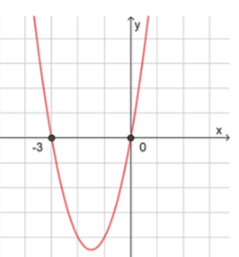
в) :
;
, значит ветви направлены вверх;
2) Нули функции:
, отсюда ;
, отсюда ;
3 Схематический рисунок:
Ответ: .
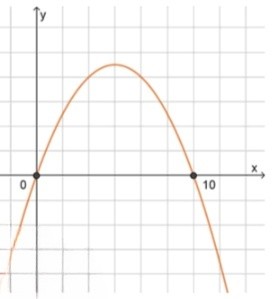
г) :
;
, значит ветви направлены вниз;
2) Нули функции:
, отсюда ;
, отсюда ;
3) Схематический рисунок:
Ответ: .
а) :
, то есть неравенство эквивалентно .
: ветви параболы направлены вниз, значит многочлен положителен строго между корнями и отрицателен вне.
Нули функции из . Умножим на (знак решения не меняется, так как это уравнение): . Дискриминант . Корни , то есть , .
Факторизация . Точки разбиения числовой оси: , .
Знак на интервалах: при имеем , , произведение ; при имеем , , произведение ; при имеем , , произведение .
Требуется , концы и не входят (строгое неравенство).
Ответ: .
б) :
, то есть неравенство эквивалентно .
: ветви параболы направлены вниз, многочлен вне промежутка между корнями и равен нулю в корнях.
Нули функции из : ; .
Порядок корней: . Точки разбиения: , .
Знак на интервалах: при имеем , , произведение ; при имеем , , произведение ; при имеем , , произведение .
Требуется : берём области, где произведение , и добавляем точки, где произведение (корни).
Ответ: .
в) :
, множитель на знак не влияет, поэтому эквивалентно анализу .
Нули из : , .
Порядок корней: . Точки разбиения: , .
Знак на интервалах: при имеем и , произведение ; при имеем , , произведение ; при имеем , , произведение .
Требуется : берём области, где произведение , и добавляем точки и , где произведение .
Ответ: .
г) :
, множитель знак не меняет, эквивалентно анализу .
Нули из : (из ), (из ).
Точки разбиения: , .
Знак на интервалах: при имеем , , произведение ; при имеем , , произведение ; при имеем , , произведение .
Требуется строго : концы и исключаются.
Ответ: .




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!