
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 298 Дорофеев, Суворова — Подробные Ответы
а) ;
б) ;
в) ;
г) ;
д) ;
е) .
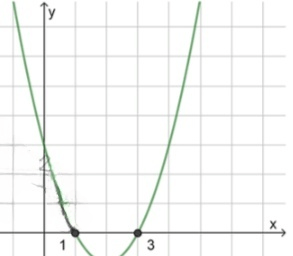
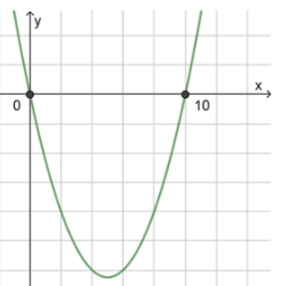
а) :
;
, значит ветви направлены вверх;
2) Нули функции:
, отсюда ;
, отсюда ;
3) Схематический рисунок:
Ответ: .
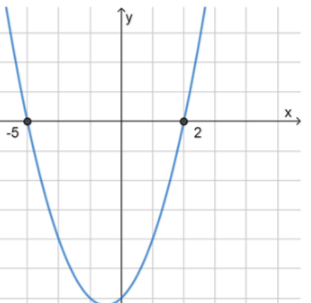
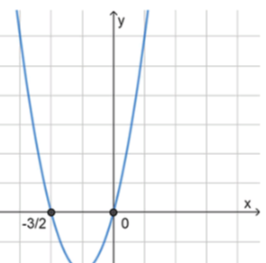
б) :
;
, значит ветви направлены вверх;
2) Нули функции:
, отсюда ;
, отсюда ;
3) Схематический рисунок:
Ответ: .
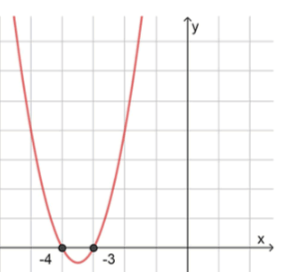
в) :
;
, значит ветви направлены вверх;
2) Нули функции:
, отсюда ;
, отсюда ;
3) Схематический рисунок:
Ответ: .
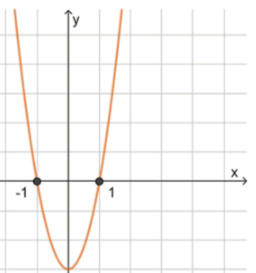
г) :
;
, значит ветви направлены вверх;
2) Нули функции:
, отсюда ;
, отсюда ;
3) Схематический рисунок:
Ответ: .
д) :
;
, значит ветви направлены вверх;
2) Нули функции:
, отсюда ;
, отсюда ;
3) Схематический рисунок:
Ответ: .
е) :
;
, значит ветви направлены вверх;
2) Нули функции:
;
, отсюда ;
3) Схематический рисунок:
Ответ: .
а) :
Эквивалентное преобразование произведения к стандартному квадратному виду: , следовательно имеем неравенство .
Коэффициент , значит парабола направлена вверх; следовательно, выражение неположительно на отрезке между нулями функции и положительно вне его.
Нули функции находятся из . Дискриминант , корни по формуле , то есть , .
Упорядочим корни ; интервалы разбиения числовой оси: , , .
Знак на интервалах (можно проверить подстановкой точек, например , , ): при значение , при значение , в точках и значение .
Требуется , поэтому берём внутренний промежуток, где , и добавляем корни, где .
Ответ: .
б) :
Приведём к квадратному виду: , то есть .
Коэффициент : парабола направлена вверх; значит вне промежутка между корнями и внутри.
Нули из . Дискриминант . Корни , то есть , .
Интервалы разбиения: , , .
Знак на интервалах (проверка точками , , ): снаружи корней , между корнями .
Требуется строго , следовательно корни не включаются.
Ответ: .
в) :
Вынесем общий множитель: , получаем . Поскольку множитель на знак не влияет, эквивалентно .
Нули произведения: ; . Упорядочим: .
Так как эквивалентный квадратный трёхчлен имеет , он на внешних промежутках относительно корней и между ними.
Интервалы: , , . Проверка точками , , подтверждает: вне произведение , внутри .
Требуется , значит включаем также точки и , где произведение равно нулю.
Ответ: .
г) :
Раскрывая скобки, можно получить , однако для знака удобнее использовать корни линейных множителей: , . Упорядочим: .
Произведение двух линейных множителей с положительным общим коэффициентом эквивалентно параболе с , а значит отрицательно строго между корнями и положительно вне.
Интервалы: , , . Проверка точками , , даёт соответственно знаки , , .
Требуется строго , концы исключаются.
Ответ: .
д) :
Выносим положительный множитель , он на знак не влияет: эквивалентно .
Нули множителей: и .
Интервалы разбиения: , , .
Знак произведения по правилу одинаковых знаков: при имеем и произведение ; при один множитель , другой произведение ; при оба множителя произведение .
Требуется строго , точки и исключаются.
Ответ: .
е) :
Можно рассматривать без раскрытия скобок: множители и .
Нули множителей: ; . Упорядочим: .
Интервалы: , , .
Знак произведения: при оба множителя произведение ; при имеем , произведение ; при оба множителя произведение . В точках и произведение равно нулю.
Требуется , следовательно берём внутренний промежуток, где , и добавляем точки нулей, где .
Ответ: .




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!