
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 296 Дорофеев, Суворова — Подробные Ответы
Решите неравенство
а)
б)
в)
г)
д)
е)
ж)
з)
и)
к)
л)
м)
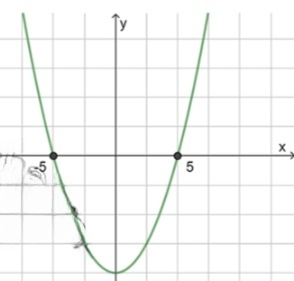
а) :
, значит ветви направлены вверх;
2) Нули функции:
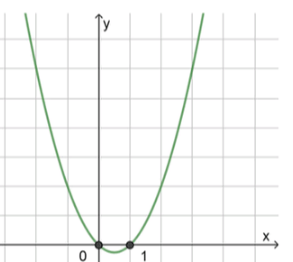
3) Схематичный рисунок:
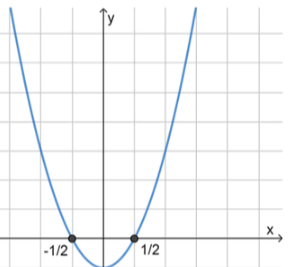
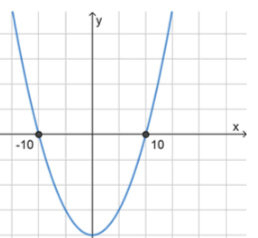
б) :
, значит ветви направлены вверх;
2) Нули функции:
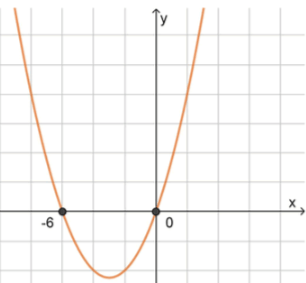
3) Схематичный рисунок:
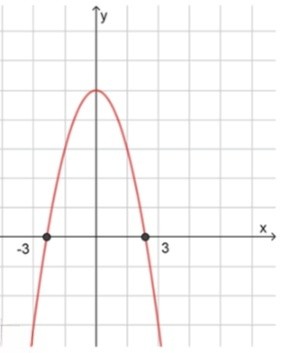
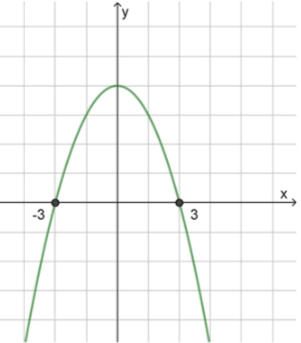
в) :
, значит ветви направлены вниз;
2) Нули функции:
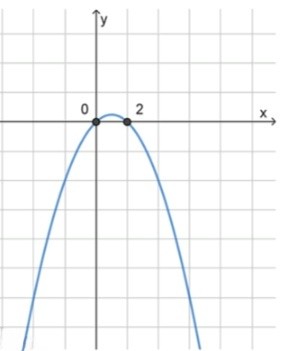
3) Схематичный рисунок:
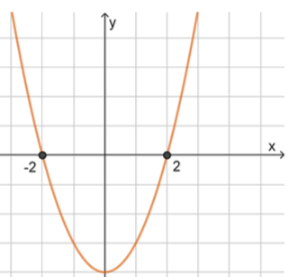
г) :
, значит ветви направлены вверх;
2) Нули функции:
3) Схематичный рисунок:
д) :
, значит ветви направлены вверх;
2) Нули функции:
3) Схематичный рисунок:
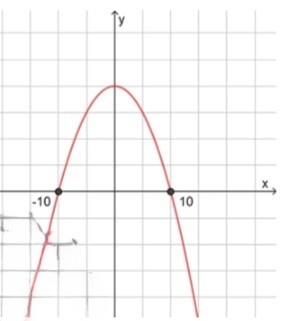
е) :
, значит ветви направлены вниз;
2) Нули функции:
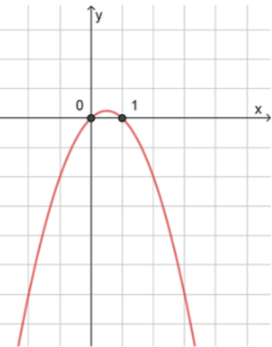
3) Схематичный рисунок:
ж) :
, значит ветви направлены вниз;
2) Нули функции:
3) Схематичный рисунок:
з) :
, значит ветви направлены вверх;
2) Нули функции:
3) Схематичный рисунок:
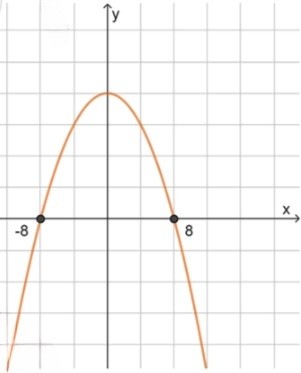
и) :
, значит ветви направлены вниз;
2) Нули функции:
3) Схематичный рисунок:
к) :
, значит ветви направлены вверх;
2) Нули функции:
3) Схематичный рисунок:
л) :
, значит ветви направлены вниз;
2) Нули функции:
3) Схематичный рисунок:
м) :
, значит ветви направлены вниз;
2) Нули функции:
3) Схематичный рисунок:
а) :
У нас есть неравенство , которое является квадратным неравенством. Чтобы решить его, сначала решим соответствующее квадратное уравнение . Это даст нам два корня:
Теперь, так как парабола с ветвями вверх (так как ), график функции пересекает ось в точках и , а на интервале между этими точками функция принимает отрицательные значения, так как парабола находится ниже оси .
Следовательно, неравенство выполняется на интервале между этими корнями:
Ответ: .
б) :
Для решения неравенства решим соответствующее квадратное уравнение:
Это уравнение можно решить следующим образом:
Парабола с ветвями вверх (так как ) пересекает ось в точках и . Между этими точками парабола находится ниже оси , то есть функция принимает отрицательные значения. Вне этих точек парабола выше оси , и функция принимает положительные значения.
Следовательно, неравенство выполняется за пределами интервала :
Ответ: .
в) :
Мы имеем неравенство . Чтобы решить его, поделим обе части на (не забывая изменить знак неравенства на противоположный):
Теперь решим соответствующее уравнение:
Парабола с ветвями вниз (так как ) имеет корни и . Неравенство выполняется за пределами этих корней, поскольку функция будет выше оси вне интервала .
Ответ:
Ответ: .
г) :
Перепишем неравенство:
Решим соответствующее квадратное уравнение:
Парабола с ветвями вверх (так как ) пересекает ось в точках и . Неравенство выполняется за пределами этих точек, то есть на интервалах и .
Ответ:
Ответ: .
д) :
Перепишем неравенство:
Раскроем скобки:
Решим это неравенство. Нули функции: и . Это означает, что функция меняет знак в этих точках. Чтобы определить, где неравенство выполняется, рассмотрим знаки на интервалах , , и :
На интервале функция отрицательна, и неравенство выполняется.
Ответ:
Ответ: .
е) :
Перепишем неравенство:
Перепишем его в виде:
Нули функции: и . Рассмотрим знаки на интервалах , , и . Неравенство выполняется на интервале .
Ответ:
Ответ: .
ж) :
Перепишем неравенство:
Нули функции: и . Рассмотрим знаки на интервалах , , и . Неравенство выполняется на интервале .
Ответ:
Ответ: .
з) :
Перепишем неравенство:
Нули функции: и . Рассмотрим знаки на интервалах , , и . Неравенство выполняется на интервалах и .
Ответ:
Ответ: .
и) :
Перепишем неравенство:
Нули функции: и . Рассмотрим знаки на интервалах , , и . Неравенство выполняется на интервалах и .
Ответ:
Ответ: .
к) :
Перепишем неравенство:
Умножим обе части на 2:
Решим:
Парабола с ветвями вверх. Неравенство выполняется на интервале .
Ответ:
Ответ: .
л) :
Перепишем неравенство:
Решим:
Парабола с ветвями вниз. Неравенство выполняется на интервале .
Ответ:
Ответ: .
м) :
Перепишем неравенство:
Умножим обе части на 10:
Решим:
Парабола с ветвями вверх. Неравенство выполняется на интервале .
Ответ:
Ответ: .




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!