ГДЗ по Алгебре 9 Класс Номер 294 Дорофеев, Суворова — Подробные Ответы

$3x^2 — 10x + 4 < 1$:
$3x^2 — 10x + 3 < 0$;

$a = 3 > 0$, значит ветви направлены вверх;

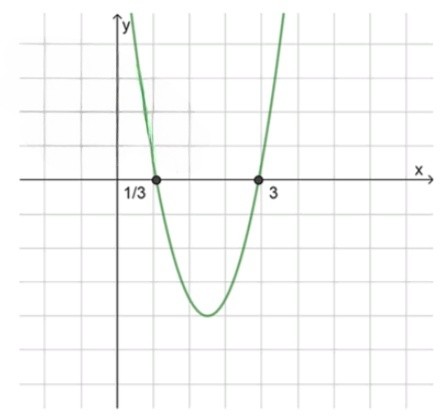
2) Нули функции:
$3x^2 — 10x + 3 = 0$;
$D = 10^2 — 4 \cdot 3 \cdot 3 = 100 — 36 = 64$, тогда:
$x_1 = \frac{10 — 8}{3 \cdot 2} = \frac{1}{3}$ и $x_2 = \frac{10 + 8}{3 \cdot 2} = 3$;

3) Схематичный рисунок:

Ответ: $\left( \frac{1}{3}; 3 \right)$.

б) $-3x^2 + 7x + 4 < -2$:
$-3x^2 + 7x + 6 < 0$;

$a = -3 < 0$, значит ветви направлены вниз;

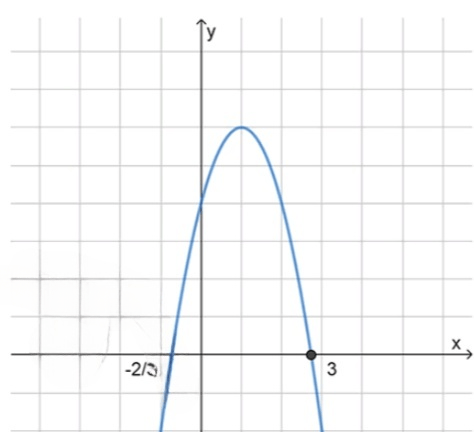
2) Нули функции:
$-3x^2 + 7x + 6 = 0$;
$D = 7^2 + 4 \cdot 3 \cdot 6 = 49 + 72 = 121$, тогда:
$x_1 = \frac{-7 — 11}{2 \cdot (-3)} = 3$ и $x_2 = \frac{-7 + 11}{2 \cdot (-3)} = -\frac{2}{3}$;

3) Схематичный рисунок:

Ответ: $(-\infty; -\frac{2}{3}) \cup (3; +\infty)$.

в) $-5x^2 + 4x + 11 > 10$:
$-5x^2 + 4x + 1 > 0$;

$a = -5 < 0$, значит ветви направлены вниз;

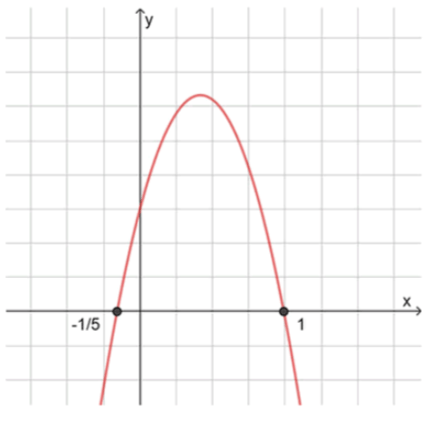
2) Нули функции:
$-5x^2 + 4x + 1 = 0$;
$D = 4^2 + 4 \cdot 5 \cdot 1 = 16 + 20 = 36$, тогда:
$x_1 = \frac{-4 — 6}{2 \cdot (-5)} = 1$ и $x_2 = \frac{-4 + 6}{2 \cdot (-5)} = -\frac{1}{5}$;

3) Схематичный рисунок:

Ответ: $\left( -\frac{1}{5}; 1 \right)$.

г) $6x^2 + 7x — 2 > -3$:
$6x^2 + 7x + 1 > 0$;

$a = 6 > 0$, значит ветви направлены вверх;

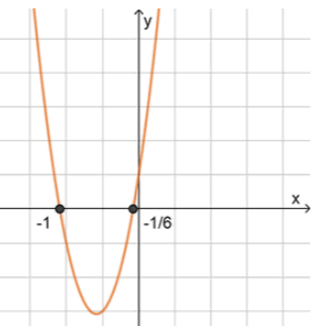
2) Нули функции:
$6x^2 + 7x + 1 = 0$;
$D = 7^2 — 4 \cdot 6 \cdot 1 = 49 — 24 = 25$, тогда:
$x_1 = \frac{-7 — 5}{2 \cdot 6} = -1$ и $x_2 = \frac{-7 + 5}{2 \cdot 6} = -\frac{1}{6}$;

3) Схематичный рисунок:

Ответ: $(-\infty; -1) \cup \left( -\frac{1}{6}; +\infty \right)$.

$3x^2 — 10x + 4 < 1$:
Эквивалентное преобразование: перенесём $1$ влево, получаем $3x^2 — 10x + 4 — 1 < 0$, то есть $3x^2 — 10x + 3 < 0$.

$a = 3 > 0$. График параболы $y = 3x^2 — 10x + 3$ направлен вверх, значит знак многочлена отрицателен строго между его корнями и положителен вне промежутка между корнями.

Для нахождения корней решим $3x^2 — 10x + 3 = 0$. Здесь $a = 3$, $b = -10$, $c = 3$. Дискриминант $D = b^2 — 4ac = (-10)^2 — 4 \cdot 3 \cdot 3 = 100 — 36 = 64$. Поскольку $D > 0$, уравнение имеет два различных вещественных корня. По формуле корней $x = \frac{-b \pm \sqrt{D}}{2a} = \frac{-(-10) \pm \sqrt{64}}{2 \cdot 3} = \frac{10 \pm 8}{6}$. Тогда $x_1 = \frac{10 — 8}{6} = \frac{2}{6} = \frac{1}{3}$, $x_2 = \frac{10 + 8}{6} = \frac{18}{6} = 3$.

Факторизация: $3x^2 — 10x + 3 = 3 \left( x — \frac{1}{3} \right) \left( x — 3 \right)$. На оси $x$ критические точки $x = \frac{1}{3}$ и $x = 3$ делят её на интервалы $(-\infty; \frac{1}{3})$, $\left( \frac{1}{3}; 3 \right)$, $(3; +\infty)$. Знак произведения при $a>0$: снаружи корней $>0$, между корнями $<0$.

Так как требуется $3x^2 — 10x + 3 < 0$, берём ровно промежуток, где выражение отрицательно, концы не входят из-за строгого неравенства.
Ответ: $\left( \frac{1}{3}; 3 \right)$.

б) $-3x^2 + 7x + 4 < -2$:
Эквивалентное преобразование: перенесём $-2$ влево, получаем $-3x^2 + 7x + 4 + 2 < 0$, то есть $-3x^2 + 7x + 6 < 0$.

$a = -3 < 0$. График параболы $y = -3x^2 + 7x + 6$ направлен вниз, значит знак многочлена положителен строго между корнями и отрицателен вне промежутка между корнями.

Для корней решим $-3x^2 + 7x + 6 = 0$. Здесь $a = -3$, $b = 7$, $c = 6$. Дискриминант $D = b^2 — 4ac = 7^2 — 4 \cdot (-3) \cdot 6 = 49 + 72 = 121$. Тогда $x = \frac{-b \pm \sqrt{D}}{2a} = \frac{-7 \pm 11}{2 \cdot (-3)} = \frac{-7 \pm 11}{-6}$. Отсюда $x_1 = \frac{-7 — 11}{-6} = \frac{-18}{-6} = 3$, $x_2 = \frac{-7 + 11}{-6} = \frac{4}{-6} = -\frac{2}{3}$. Упорядочим: меньший корень $-\frac{2}{3}$, больший корень $3$.

Факторизация: $-3x^2 + 7x + 6 = -3 \left( x + \frac{2}{3} \right) \left( x — 3 \right)$. Интервалы: $(-\infty; -\frac{2}{3})$, $\left( -\frac{2}{3}; 3 \right)$, $(3; +\infty)$. При $a<0$ знак $<0$ наблюдается вне промежутка между корнями.

Требуется $-3x^2 + 7x + 6 < 0$, значит берём внешние интервалы, концы исключаем.

Ответ: $(-\infty; -\frac{2}{3}) \cup (3; +\infty)$.

в) $-5x^2 + 4x + 11 > 10$:
Эквивалентное преобразование: перенесём $10$ влево, получаем $-5x^2 + 4x + 11 — 10 > 0$, то есть $-5x^2 + 4x + 1 > 0$.

$a = -5 < 0$. Для параболы, направленной вниз, многочлен $>0$ строго между корнями и $<0$ вне.

Находим корни уравнения $-5x^2 + 4x + 1 = 0$. Здесь $a = -5$, $b = 4$, $c = 1$. Дискриминант $D = b^2 — 4ac = 4^2 — 4 \cdot (-5) \cdot 1 = 16 + 20 = 36$. Тогда $x = \frac{-b \pm \sqrt{D}}{2a} = \frac{-4 \pm 6}{2 \cdot (-5)} = \frac{-4 \pm 6}{-10}$. Отсюда $x_1 = \frac{-4 — 6}{-10} = \frac{-10}{-10} = 1$, $x_2 = \frac{-4 + 6}{-10} = \frac{2}{-10} = -\frac{1}{5}$. Упорядочим: $-\frac{1}{5} < 1$.

Факторизация: $-5x^2 + 4x + 1 = -5 \left( x + \frac{1}{5} \right) \left( x — 1 \right)$. Интервалы: $(-\infty; -\frac{1}{5})$, $\left( -\frac{1}{5}; 1 \right)$, $(1; +\infty)$. При $a<0$ выражение $>0$ между корнями.

Требуется $-5x^2 + 4x + 1 > 0$, значит берём промежуток между корнями, концы исключаем.

Ответ: $\left( -\frac{1}{5}; 1 \right)$.

г) $6x^2 + 7x — 2 > -3$:
Эквивалентное преобразование: перенесём $-3$ влево, получаем $6x^2 + 7x — 2 + 3 > 0$, то есть $6x^2 + 7x + 1 > 0$.

$a = 6 > 0$. График направлен вверх, значит многочлен $>0$ вне промежутка между корнями и $<0$ только между ними.

Решим $6x^2 + 7x + 1 = 0$. Здесь $a = 6$, $b = 7$, $c = 1$. Дискриминант $D = b^2 — 4ac = 7^2 — 4 \cdot 6 \cdot 1 = 49 — 24 = 25$. Тогда $x = \frac{-b \pm \sqrt{D}}{2a} = \frac{-7 \pm 5}{2 \cdot 6} = \frac{-7 \pm 5}{12}$. Отсюда $x_1 = \frac{-7 — 5}{12} = \frac{-12}{12} = -1$, $x_2 = \frac{-7 + 5}{12} = \frac{-2}{12} = -\frac{1}{6}$.

Факторизация: $6x^2 + 7x + 1 = 6 \left( x + 1 \right) \left( x + \frac{1}{6} \right)$. Интервалы: $(-\infty; -1)$, $\left( -1; -\frac{1}{6} \right)$, $\left( -\frac{1}{6}; +\infty \right)$. При $a>0$ выражение $>0$ вне промежутка между корнями.

Требуется $6x^2 + 7x + 1 > 0$, значит берём внешние интервалы, концы исключаем.

Ответ: $(-\infty; -1) \cup \left( -\frac{1}{6}; +\infty \right)$.