
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 293 Дорофеев, Суворова — Подробные Ответы
а) ;
б) ;
в) ;
г) .
а) :
, значит ветви направлены вниз;
2) Нули функции:
;
;
, отсюда ;
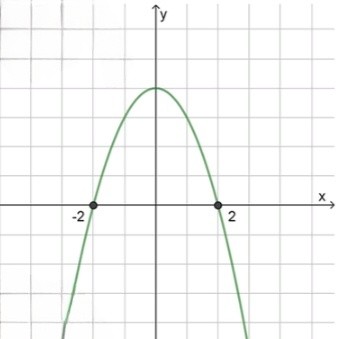
3) Схематический рисунок:
б) :
, значит ветви направлены вниз;
2) Нули функции:
;
, тогда:
и ;
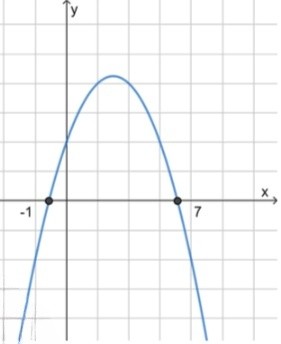
3) Схематический рисунок:
в) :
, значит ветви направлены вниз;
2) Нули функции:
;
;
, отсюда ;
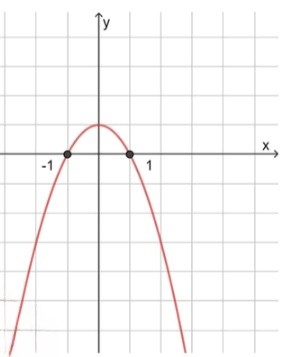
3) Схематический рисунок:
а) :
Мы имеем неравенство . Это квадратное неравенство. Вначале решим соответствующее квадратное уравнение, приравняв к нулю, чтобы найти корни, которые определят границы области решения:
Перепишем уравнение, из которого мы будем находить корни:
Теперь решим его относительно :
Отсюда получаем два возможных значения для :
Таким образом, корни уравнения — и .
Теперь решим неравенство. Мы знаем, что для параболы с ветвями вниз (так как коэффициент ), область, где функция положительна, будет между корнями. Это интервал от до :
Ответ: .
б) :
Рассмотрим неравенство . Как и в предыдущем случае, для решения сначала найдем корни соответствующего квадратного уравнения:
Перепишем уравнение, приравняв его к нулю:
Теперь найдем дискриминант ():
Так как дискриминант положительный, у нас два различных корня:
Рассчитаем корни:
Теперь исследуем, что происходит с функцией на интервалах. Парабола с ветвями вниз (так как коэффициент ) будет положительной между корнями. Таким образом, неравенство выполняется на интервале:
Ответ: .
в) :
Рассмотрим неравенство . Для решения приравняем выражение к нулю:
Решим это уравнение относительно :
Отсюда получаем два корня:
То есть, и .
Для неравенства функция будет отрицательной за пределами этих корней, так как парабола открыта вниз. Таким образом, решение будет на интервалах и :
Ответ: .




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!