
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 291 Дорофеев, Суворова — Подробные Ответы
Вычислите абсциссы точек пересечения параболы с осью , изобразите параболу схематически и отметьте на оси значения аргумента, при которых:
;
;
.
В каждом случае проверьте себя, подставив в формулу какое-нибудь значение из найденного множества.
а) ;
б) ;
в) ;
г) ;
д) ;
е) .
а) :
, значит ветви направлены вверх;
2) Нули функции:
3) Схематический рисунок:
- Если , то ;
- Если или , то ;
4) Проверка подстановкой:
б) :
, значит ветви направлены вниз;
2) Нули функции:
3) Схематический рисунок:
- Если , то ;
- Если или , то ;
4) Проверка подстановкой:
в) :
, значит ветви направлены вверх;
2) Нули функции:
3) Схематический рисунок:
- Если , то ;
- Если или , то ;
4) Проверка подстановкой:
г) :
, значит ветви направлены вверх;
2) Нули функции:
3) Схематический рисунок:
- Если , то ;
- Если или , то ;
4) Проверка подстановкой:
д) :
, значит ветви направлены вверх;
2) Нули функции:
3) Схематический рисунок:
- Если , то ;
- Если или , то ;
4) Проверка подстановкой:
е) :
, значит ветви направлены вниз;
2) Нули функции:
3) Схематический рисунок:
- Если , то ;
- Если или , то ;
4) Проверка подстановкой:
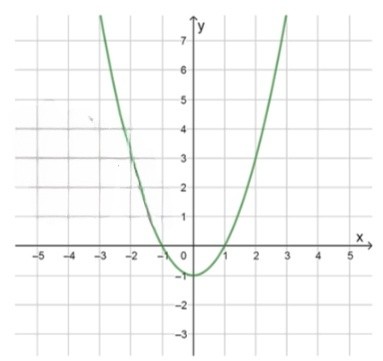
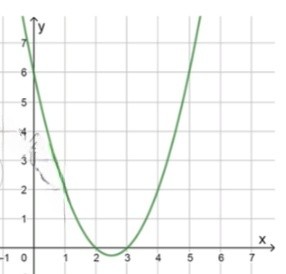
а) :
, значит ветви направлены вверх;
Так как коэффициент при равен 1, это положительное число, то парабола будет открываться вверх. Это значит, что её вершина будет минимальной, а парабола будет расти по обеим сторонам от неё.
Нули функции:
Для того чтобы найти нули функции, нужно решить уравнение :
Таким образом, нули функции находятся в точках и . Это означает, что график функции пересекает ось в этих точках.
Схематический рисунок:
Если , то ;
Между и , когда находится в этом интервале, парабола лежит ниже оси , то есть значения функции отрицательны. Например, для , , что подтверждает, что .
Если или , то ;
Для значений , находящихся вне интервала , функция лежит выше оси , и соответственно значения положительны. Например, для , , и для , .
Проверка подстановкой:
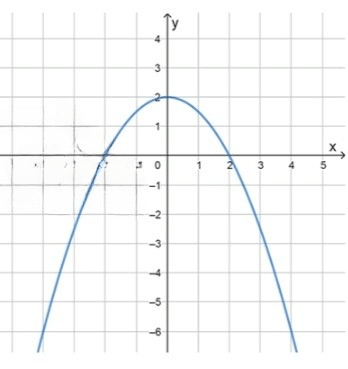
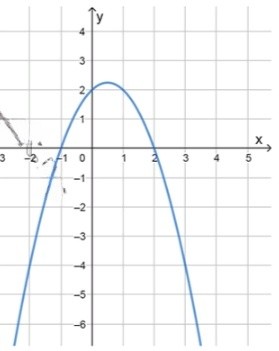
б) :
, значит ветви направлены вниз;
Здесь коэффициент при отрицателен, это означает, что парабола открывается вниз, а её вершина будет максимальной. График функции будет иметь вид «горы», а не «ямы», как в случае с положительным коэффициентом.
Нули функции:
Чтобы найти нули функции, решим уравнение :
Умножим обе стороны на -2, чтобы избавиться от дроби:
Нули функции находятся в точках и , то есть график функции пересекает ось в этих точках.
Схематический рисунок:
Если , то ;
Между точками пересечения с осью функция находится выше оси , что даёт положительные значения для . Например, для , .
Если или , то ;
Вне интервала функция находится ниже оси , что даёт отрицательные значения для . Например, для , , и для , .
Проверка подстановкой:
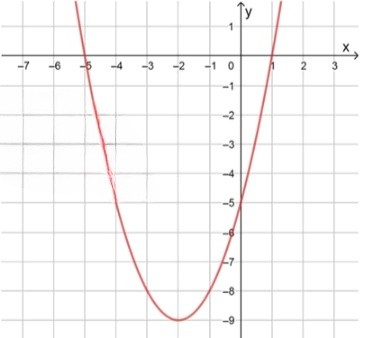
в) :
, значит ветви направлены вверх;
Как и в предыдущих примерах, коэффициент при положительный, следовательно, парабола открывается вверх, а её вершина будет минимальной.
Нули функции:
Чтобы найти нули функции, решим уравнение :
Дискриминант:
Тогда корни:
Нули функции находятся в точках и , то есть график функции пересекает ось в этих точках.
Схематический рисунок:
Если , то ;
Между точками пересечения с осью функция находится ниже оси , что даёт отрицательные значения для . Например, для , , что подтверждает, что .
Если или , то ;
Вне этих интервалов функция находится выше оси , что даёт положительные значения для . Например, для , , и для , .
Проверка подстановкой:
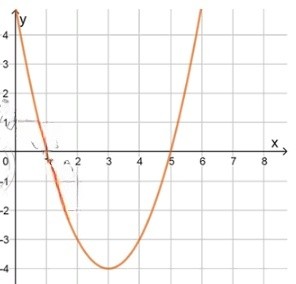
г) :
, значит ветви направлены вверх;
Как и в предыдущих примерах, коэффициент при положительный, следовательно, парабола открывается вверх.
Нули функции:
Чтобы найти нули функции, решим уравнение :
Дискриминант:
Тогда корни:
Нули функции находятся в точках и , то есть график функции пересекает ось в этих точках.
Схематический рисунок:
Если , то ;
Между точками пересечения с осью , функция находится ниже оси , что даёт отрицательные значения для .
Если или , то ;
Вне этого интервала функция находится выше оси , что даёт положительные значения для .
Проверка подстановкой:
д) :
, значит ветви направлены вверх;
Здесь парабола также открывается вверх, так как коэффициент при положительный.
Нули функции:
Чтобы найти нули функции, решим уравнение :
Дискриминант:
Тогда корни:
Нули функции находятся в точках и , то есть график функции пересекает ось в этих точках.
Схематический рисунок:
Если , то ;
Между точками пересечения с осью , функция находится ниже оси , что даёт отрицательные значения для .
Если или , то ;
Вне этого интервала функция находится выше оси , что даёт положительные значения для .
Проверка подстановкой:
е) :
, значит ветви направлены вниз;
Парабола открывается вниз, так как коэффициент при отрицателен, и её вершина будет максимальной.
Нули функции:
Чтобы найти нули функции, решим уравнение :
Дискриминант:
Тогда корни:
Нули функции находятся в точках и , то есть график функции пересекает ось в этих точках.
Схематический рисунок:
Если , то ;
Между корнями функция находится выше оси , давая положительные значения для .
Если или , то ;
Вне этих интервалов функция находится ниже оси , что даёт отрицательные значения для .
Проверка подстановкой:




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!