ГДЗ по Алгебре 9 Класс Номер 287 Дорофеев, Суворова — Подробные Ответы

Сумма катетов прямоугольного треугольника равна 8. Задайте формулой зависимость площади S прямоугольного треугольника от длины катета х (рис. 2.40). Определите, при каком значении х треугольник имеет наибольшую площадь. Дайте геометрическое истолкование вашего ответа.

$P = 8 \, \text{см}$ — сумма катетов треугольника;
$S$ — площадь треугольника;
$a = x$ — длина катета;

1) Уравнение зависимости площади $S$ от длины $x$ катета:
$b = 8 — x \, (\text{см})$ — длина второго катета;

$$S = \frac{1}{2}ab = \frac{1}{2}x(8 — x);$$ $$S = 4x — \frac{1}{2}x^2;$$

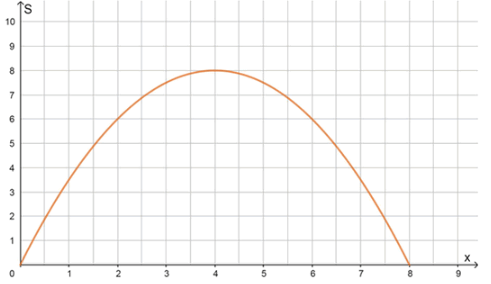
2) График зависимости площади от длины катета:

3) График имеет форму параболы с ветвями, направленными вниз, значит максимальная площадь треугольника достигается в ее вершине:

$$a=x=-\frac{4}{2\cdot (-0.5)}=\frac{4}{1}=4\text{см};$$

$$a = x = -\frac{4}{2 \cdot (-0.5)} = \frac{4}{1} = 4 \, \text{см};$$ $$b = (8 — x) = 8 — 4 = 4 \, \text{см};$$

4) Из всех прямоугольных треугольников с данной суммой длин катетов наибольшую площадь имеет равнобедренный;

Ответ: при $x = 4$.

$P = 8 \, \text{см}$ — сумма катетов треугольника;
$S$ — площадь треугольника;
$a = x$ — длина катета;

1) Уравнение зависимости площади $S$ от длины $x$ катета:
Периметр прямоугольного треугольника равен сумме всех его сторон, а площадь прямоугольного треугольника можно выразить через его катеты как $S = \frac{1}{2} \cdot a \cdot b$, где $a$ и $b$ — катеты треугольника. В данном случае $a = x$ и $b = 8 — x$, поскольку сумма катетов $P = a + b = 8$. Подставляем это в формулу для площади:

$$S = \frac{1}{2} \cdot a \cdot b = \frac{1}{2} \cdot x \cdot (8 — x)$$

Раскрываем скобки:

$$S = \frac{1}{2} \cdot (8x — x^2)$$

Преобразуем:

$$S = 4x — \frac{1}{2} x^2$$

2) График зависимости площади от длины катета:
Для того чтобы построить график функции площади $S(x)$, вычислим несколько значений площади для различных значений катета $x$. В таблице представлены значения $x$ от 0 до 8 и соответствующие площади:

Для $x = 0$:

$$S = 4 \cdot 0 — \frac{1}{2} \cdot 0^2 = 0$$

Для $x = 2$:

$$S = 4 \cdot 2 — \frac{1}{2} \cdot 2^2 = 8 — 2 = 6$$

Для $x = 4$:

$$S = 4 \cdot 4 — \frac{1}{2} \cdot 4^2 = 16 — 8 = 8$$

Для $x = 6$:

$$S = 4 \cdot 6 — \frac{1}{2} \cdot 6^2 = 24 — 18 = 6$$

Для $x = 8$:

$$S = 4 \cdot 8 — \frac{1}{2} \cdot 8^2 = 32 — 32 = 0$$

3) График имеет форму параболы с ветвями, направленными вниз, что означает, что максимальная площадь треугольника достигается в вершине параболы. Для нахождения абсциссы вершины параболы, которая для квадратичной функции $S(x) = ax^2 + bx + c$ определяется по формуле:

$$x_{\text{max}} = -\frac{b}{2a}$$

В уравнении для площади $S = -\frac{1}{2}x^2 + 4x$ коэффициент $a = -\frac{1}{2}$, $b = 4$. Подставляем эти значения в формулу для вершины:

$$x_{\text{max}} = -\frac{4}{2 \cdot \left(-\frac{1}{2}\right)} = \frac{4}{1} = 4$$

Таким образом, максимальная площадь треугольника достигается при $x = 4$.

4) Теперь, зная, что максимальная площадь треугольника достигается при $x = 4$, вычислим длину второго катета $b$. Из уравнения $b = 8 — x$ при $x = 4$ получаем:

$$b = 8 — 4 = 4$$

Таким образом, при $x = 4$ второй катет также имеет длину 4 см, и треугольник является равнобедренным.

Из всех прямоугольных треугольников с данной суммой длин катетов наибольшую площадь имеет равнобедренный треугольник, где оба катета равны. Ответ: при $x = 4$.