ГДЗ по Алгебре 9 Класс Номер 286 Дорофеев, Суворова — Подробные Ответы

Площадь прямоугольника S с периметром, равным 16 см, является функцией длины его основания х. Задайте эту функцию формулой. Определите, при каком значении х функция принимает наибольшее значение. Дайте геометрическое истолкование вашего ответа.

$P = 16 \, \text{см}$ — периметр прямоугольника;
$S$ — площадь прямоугольника;
$x$ — длина основания;

1) Уравнение зависимости площади $S$ от длины $x$ основания:
Пусть $a = x$ — одна из сторон прямоугольника и $b$ — вторая сторона;
$P = 2(a + b)$, отсюда $b = \frac{P}{2} — a = \frac{16}{2} — x = 8 — x$;
$S = ab = x(8 — x)$;
$S = 8x — x^2$;

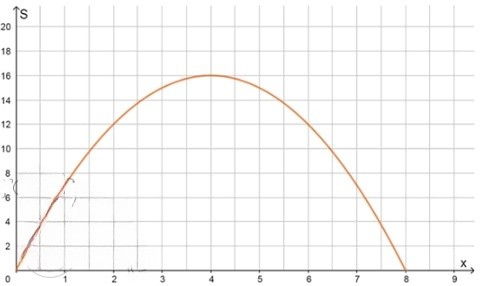
2) График зависимости площади от длины основания:

3) График имеет форму параболы с ветвями, направленными вниз, значит максимальная площадь прямоугольника достигается в ее вершине:
$a = x = -\frac{8}{2 \cdot (-1)} = \frac{8}{2} = 4 \, \text{см}$;
$b = (8 — x) = 8 — 4 = 4 \, \text{см}$;

4) Из всех прямоугольников с данным периметром наибольшую площадь имеет квадрат;

Ответ: при $x = 4$.

$P = 16 \, \text{см}$ — периметр прямоугольника;
$S$ — площадь прямоугольника;
$x$ — длина основания;

1) Уравнение зависимости площади $S$ от длины $x$ основания:
Для прямоугольника периметр выражается через его стороны $a$ и $b$ как $P = 2(a + b)$. В нашем случае одна из сторон прямоугольника $a$ равна $x$, и для второй стороны $b$ можно выразить её через $x$, используя формулу для периметра:

$$P = 2(x + b)$$

Подставляем $P = 16$:

$$16 = 2(x + b)$$

Делим обе части на 2:

$$8 = x + b$$

Из этого выражения находим $b$:

$$b = 8 — x$$

Теперь, зная выражение для $b$, можем найти площадь прямоугольника. Площадь прямоугольника равна произведению его сторон $a$ и $b$, то есть:

$$S = a \cdot b$$

Подставляем $a = x$ и $b = 8 — x$:

$$S = x(8 — x)$$

Раскрываем скобки:

$$S = 8x — x^2$$

2) График зависимости площади от длины основания:
Для того чтобы построить график зависимости площади от длины основания, нужно вычислить несколько значений площади для разных значений $x$. Вот таблица значений для $x$ от 0 до 8:

Для $x = 0$:

$$S = 8 \cdot 0 — (0)^2 = 0$$

Для $x = 2$:

$$S = 8 \cdot 2 — (2)^2 = 16 — 4 = 12$$

Для $x = 4$:

$$S = 8 \cdot 4 — (4)^2 = 32 — 16 = 16$$

Для $x = 6$:

$$S = 8 \cdot 6 — (6)^2 = 48 — 36 = 12$$

Для $x = 8$:

$$S = 8 \cdot 8 — (8)^2 = 64 — 64 = 0$$

3) График имеет форму параболы с ветвями, направленными вниз, что означает, что максимальная площадь прямоугольника достигается в вершине параболы. Для нахождения вершины параболы нужно найти значение $x$, при котором площадь максимальна. Для этого используется формула для абсциссы вершины параболы, которая для квадратичной функции $S(x) = ax^2 + bx + c$ имеет вид:

$$x_{\text{max}} = -\frac{b}{2a}$$

В нашем уравнении $S = -x^2 + 8x$, коэффициент $a = -1$, $b = 8$. Подставляем в формулу:

$$x_{\text{max}} = -\frac{8}{2 \cdot (-1)} = \frac{8}{2} = 4$$

4) Теперь, зная, что максимальная площадь достигается при $x = 4$, найдем соответствующие значения для сторон прямоугольника. Если $x = 4$, то вторая сторона $b$ будет равна:

$$b = 8 — 4 = 4$$

Таким образом, прямоугольник становится квадратом с длиной стороны $4 \, \text{см}$.

Из всех прямоугольников с данным периметром наибольшую площадь имеет квадрат, так как в случае квадрата обе стороны равны, и площадь максимальна. Ответ: при $x = 4$.