ГДЗ по Алгебре 9 Класс Номер 285 Дорофеев, Суворова — Подробные Ответы

Футболист на тренировке подбрасывает мяч ногой вертикально вверх с начальной скоростью 15 м/с. На какую максимальную высоту поднимется мяч?

$h_0 = 0 \, \text{м}$ — начальная высота;
$v_0 = 15 \, \text{м/с}$ — начальная скорость мяча;
$g = 9.8 \, \text{м/с}^2$ — ускорение свободного падения;

1) Уравнение зависимости высоты $h$ мяча от времени $t$ полета:
$h = -\frac{1}{2}gt^2 + v_0t + h_0$;
$h = -\frac{1}{2} \cdot 9.8 \cdot t^2 + 15 \cdot t + 0$;
$h = -4.9t^2 + 15t$;

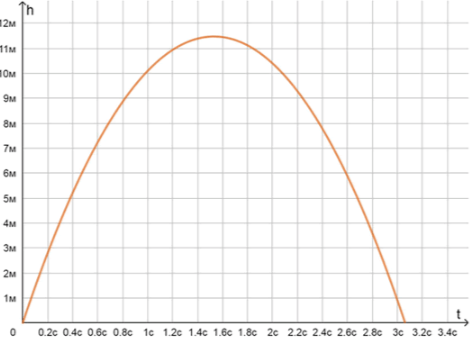
2) График зависимости высоты от времени полета:

3) График имеет форму параболы с ветвями, направленными вниз, значит максимальная высота подъема мяча достигается в ее вершине:
$t = -\frac{15}{2 \cdot (-4.9)} = \frac{15}{9.8} \approx 1.5$;
$h = -4.9 \cdot (1.5)^2 + 15 \cdot 1.5 \approx -4.9 \cdot 2.25 + 22.5 \approx -11 + 22.5 \approx 11.5$;

Ответ: $\approx 11.5 \, \text{м}$.

$h_0 = 0 \, \text{м}$ — начальная высота;
$v_0 = 15 \, \text{м/с}$ — начальная скорость мяча;
$g = 9.8 \, \text{м/с}^2$ — ускорение свободного падения;

1) Уравнение зависимости высоты $h$ мяча от времени $t$ полета:
Для описания движения мяча в условиях свободного падения используется уравнение, описывающее изменение высоты с течением времени. Это уравнение является результатом применения второго закона Ньютона к телам, движущимся с постоянным ускорением, и имеет вид:

$$h = -\frac{1}{2} g t^2 + v_0 t + h_0$$

где $h$ — высота мяча в момент времени $t$, $g$ — ускорение свободного падения, $v_0$ — начальная скорость мяча, $h_0$ — начальная высота мяча. Подставим известные значения $g = 9.8 \, \text{м/с}^2$, $v_0 = 15 \, \text{м/с}$, $h_0 = 0 \, \text{м}$:

$$h = -\frac{1}{2} \cdot 9.8 \cdot t^2 + 15 \cdot t + 0$$ $$h = -4.9 t^2 + 15 t$$

2) График зависимости высоты от времени полета:
Для получения графика функции $h(t)$, необходимо вычислить значения $h$ для различных значений $t$. В табличной форме это выглядит следующим образом:

В данной таблице значения $t$ представляют собой моменты времени, в которых высота мяча определяется с помощью уравнения. Для каждого значения $t$ вычисляется соответствующее значение $h$, которое отображает высоту мяча в этот момент времени. Например, для $t = 0,4$ секунды:

$$h = -4.9 \cdot (0.4)^2 + 15 \cdot 0.4 = -4.9 \cdot 0.16 + 6 = -0.784 + 6 = 5.2 \, \text{м}$$

Для $t = 0,8$ секунды:

$$h = -4.9 \cdot (0.8)^2 + 15 \cdot 0.8 = -4.9 \cdot 0.64 + 12 = -3.136 + 12 = 8.8 \, \text{м}$$

Подобным образом можно вычислить высоту для остальных значений $t$, что приведет к таблице выше.

3) График имеет форму параболы с ветвями, направленными вниз, что означает, что максимальная высота подъема мяча достигается в вершине параболы. Для нахождения времени $t_{\text{max}}$, когда достигается максимальная высота, нужно найти вершину параболы. Это можно сделать, используя формулу для времени вершины параболы, которая для квадратичной функции $h(t) = at^2 + bt + c$ имеет вид:

$$t_{\text{max}} = -\frac{b}{2a}$$

где $a = -4.9$, $b = 15$. Подставляем значения:

$$t_{\text{max}} = -\frac{15}{2 \cdot (-4.9)} = \frac{15}{9.8} \approx 1.5 \, \text{с}$$

Теперь подставим это значение времени в уравнение для высоты, чтобы найти максимальную высоту $h_{\text{max}}$:

$$h_{\text{max}} = -4.9 \cdot (1.5)^2 + 15 \cdot 1.5$$ $$h_{\text{max}} = -4.9 \cdot 2.25 + 22.5 = -11.025 + 22.5 = 11.475 \, \text{м}$$

Таким образом, максимальная высота, которую достигает мяч, равна $\approx 11.5 \, \text{м}$.