
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 283 Дорофеев, Суворова — Подробные Ответы
Даны функции вида: ;
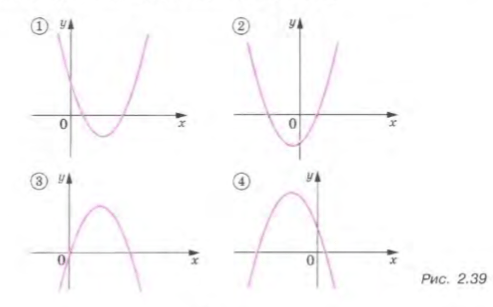
1) Ветви направлены вверх, значит ;
Координата вершины положительна, значит ;
Пересекает ось выше оси , значит (, тогда );
2) Ветви направлены вверх, значит ;
Координата вершины отрицательна, значит ;
Пересекает ось ниже оси , значит (, тогда );
3) Ветви направлены вниз, значит ;
Координата вершины положительна, значит ;
Проходит через начало координат, значит (, тогда );
4) Ветви направлены вниз, значит ;
Координата вершины отрицательна, значит ;
Пересекает ось выше оси , значит (, тогда ).
1) Ветви направлены вверх, значит :
Уравнение параболы имеет вид , где коэффициент определяет направление ветвей параболы. Если , то парабола будет направлена вверх. В случае, когда , ветви параболы будут подниматься вверх, и вершина будет находиться в нижней части графика.
Координата вершины параболы определяется по формуле:
В данном случае, если вершина параболы лежит справа от оси , то координата будет положительной. Это означает, что для того, чтобы вершина параболы находилась справа от оси , коэффициент должен быть отрицательным. Таким образом, если и , то для того, чтобы это условие выполнялось, необходимо, чтобы .
Пересекает ось выше оси , значит :
При , значение функции будет равно . Если парабола пересекает ось выше оси , то значение должно быть положительным. Это означает, что . Таким образом, если парабола пересекает ось выше оси , то коэффициент будет положительным.
2) Ветви направлены вверх, значит :
Если парабола направлена вверх, то значение должно быть положительным, как мы уже объясняли в предыдущем пункте.
Координата вершины параболы отрицательная, значит :
Когда вершина параболы находится слева от оси , то координата будет отрицательной. Если и , то для этого должно быть положительным. Это можно объяснить тем, что при , если вершина находится слева от оси , то коэффициент должен быть положительным, чтобы значение было отрицательным.
Пересекает ось ниже оси , значит :
Если парабола пересекает ось ниже оси , то при , значение будет отрицательным, что означает, что коэффициент должен быть отрицательным. Таким образом, .
3) Ветви направлены вниз, значит :
Если ветви параболы направлены вниз, то значение должно быть отрицательным. В случае, когда , парабола будет направлена вниз, и вершина будет находиться в верхней части графика.
Координата вершины положительная, значит :
Когда парабола направлена вниз, координата вершины будет положительной, если коэффициент положителен. Это объясняется тем, что вершина будет находиться справа от оси при , и если , то при таком значении , вершина параболы будет слева от оси .
Проходит через начало координат, значит :
Если парабола проходит через начало координат, это означает, что при , значение . Это подразумевает, что . То есть, если парабола проходит через начало координат, то значение будет равно нулю.
4) Ветви направлены вниз, значит :
Если ветви параболы направлены вниз, то должно быть отрицательным, как объяснялось ранее.
Координата вершины отрицательная, значит :
Когда вершина параболы находится слева от оси , то координата будет отрицательной. При и , это означает, что для того, чтобы вершина находилась слева, должно быть отрицательным. Таким образом, если вершина параболы находится слева от оси , то .
Пересекает ось выше оси , значит :
Если парабола пересекает ось выше оси , то при , значение будет положительным. Это значит, что должно быть положительным. Таким образом, если парабола пересекает ось выше оси , то .




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!