ГДЗ по Алгебре 9 Класс Номер 279 Дорофеев, Суворова — Подробные Ответы

На рисунке 2.38 изображено кольцо, радиус внешнего круга которого равен 2 см. 1) Запишите формулу, выражающую зависимость площади А кольца от его ширины x.
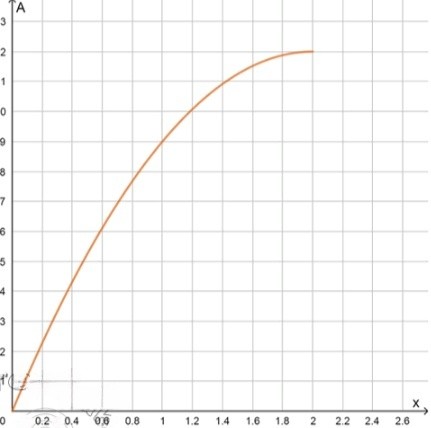
2) Начертите график зависимости А от х.
3) Какова область определения рассматриваемой функции?
4) Опишите, как меняется площадь А кольца с изменением х от 0 до 2; от 0 до 1; от 1 до 2.

$x$ — ширина кольца;
$R = 2 \, \text{см}$ — радиус внешнего круга;
Примем число $\pi$ равным 3;

1) Уравнение зависимости площади $A$ кольца от его ширины $x$:

$$r = R — x \, (\text{см}) \quad \text{— радиус внутреннего круга};$$ $$S_1 = \pi R^2 \, (\text{см}^2) \quad \text{— площадь внешнего круга};$$ $$S_2 = \pi (R — x)^2 \, (\text{см}^2) \quad \text{— площадь внутреннего круга};$$ $$A = S_1 — S_2 = \pi R^2 — \pi (R — x)^2;$$ $$A = 3 \cdot 2^2 — 3 \cdot (2 — x)^2;$$ $$A = 12 — 3 \cdot (4 — 4x + x^2);$$ $$A = 12 — 12 + 12x — 3x^2;$$ $$A = 12x — 3x^2;$$

2) График зависимости $A$ от $x$:

$$\begin{array}{|c|c|c|c|c|c|c|c|} \hline x & 0 & 0,4 & 0,8 & 1 & 1,4 & 1,8 & 2 \\ \hline A & 0 & 4,3 & 7,7 & 9 & 10,9 & 11,9 & 12 \\ \hline \end{array}$$

3) Область определения данной функции:
Ширина кольца не может быть меньше нуля, а также не может превышать радиус $R$ внешнего круга, значит $D(x) = [0; 2]$;

4) Изменение площади $A$ кольца с изменением $x$:
От 0 до 2: увеличивается от $0$ до $12 \, \text{см}^2$;
От 0 до 1: увеличивается от $0$ до $9 \, \text{см}^2$;
От 1 до 2: увеличивается от $9 \, \text{см}^2$ до $12 \, \text{см}^2$.

1) Уравнение зависимости площади $A$ кольца от его ширины $x$:

Для начала, определим площадь кольца как разницу между площадью внешнего круга и площадью внутреннего круга. Площадь круга вычисляется по формуле $S = \pi r^2$, где $r$ — радиус круга. Таким образом, площадь кольца $A$ будет равна разности двух таких площадей:

$$S_1 = \pi R^2 \quad \text{— площадь внешнего круга, где \( R \) — радиус внешнего круга;}$$ $$S_2 = \pi (R — x)^2 \quad \text{— площадь внутреннего круга, где \( x \) — радиус внутреннего круга.}$$

Теперь можем выразить площадь кольца $A$ как разницу между этими двумя площадями:

$$A = S_1 — S_2 = \pi R^2 — \pi (R — x)^2$$

Подставляем $R = 2$ и $\pi = 3$:

$$A = 3 \cdot 2^2 — 3 \cdot (2 — x)^2$$

Рассчитываем квадрат радиусов:

$$A = 3 \cdot 4 — 3 \cdot (4 — 4x + x^2)$$

Теперь раскрываем скобки:

$$A = 12 — 3 \cdot (4 — 4x + x^2)$$ $$A = 12 — 12 + 12x — 3x^2$$

Таким образом, уравнение зависимости площади кольца от его ширины $x$ имеет вид:

$$A = 12x — 3x^2$$

2) График зависимости $A$ от $x$:

Теперь вычислим площадь кольца для различных значений $x$ на интервале $[0, 2]$. Подставим значения $x = 0$, $x = 0,4$, $x = 0,8$, $x = 1$, $x = 1,4$, $x = 1,8$, $x = 2$ в уравнение $A = 12x — 3x^2$:

• Для $x = 0$:

$$A(0) = 12 \cdot 0 — 3 \cdot 0^2 = 0$$

• Для $x = 0,4$:

$$A(0,4) = 12 \cdot 0,4 — 3 \cdot (0,4)^2 = 4,8 — 3 \cdot 0,16 = 4,8 — 0,48 = 4,32$$

• Для $x = 0,8$:

$$A(0,8) = 12 \cdot 0,8 — 3 \cdot (0,8)^2 = 9,6 — 3 \cdot 0,64 = 9,6 — 1,92 = 7,68$$

• Для $x = 1$:

$$A(1) = 12 \cdot 1 — 3 \cdot (1)^2 = 12 — 3 = 9$$

• Для $x = 1,4$:

$$A(1,4) = 12 \cdot 1,4 — 3 \cdot (1,4)^2 = 16,8 — 3 \cdot 1,96 = 16,8 — 5,88 = 10,92$$

• Для $x = 1,8$:

$$A(1,8) = 12 \cdot 1,8 — 3 \cdot (1,8)^2 = 21,6 — 3 \cdot 3,24 = 21,6 — 9,72 = 11,88$$

• Для $x = 2$:

$$A(2) = 12 \cdot 2 — 3 \cdot (2)^2 = 24 — 3 \cdot 4 = 24 — 12 = 12$$

Теперь соберем все полученные данные в таблицу:

$$\begin{array}{|c|c|c|c|c|c|c|c|} \hline x & 0 & 0,4 & 0,8 & 1 & 1,4 & 1,8 & 2 \\ \hline A & 0 & 4,32 & 7,68 & 9 & 10,92 & 11,88 & 12 \\ \hline \end{array}$$

3) Область определения данной функции:

Ширина кольца $x$ не может быть меньше нуля, так как радиус внутреннего круга не может быть отрицательным. Кроме того, ширина кольца не может превышать радиус внешнего круга $R = 2$. Таким образом, область определения функции будет ограничена интервалом от 0 до 2:

$$D(x) = [0; 2]$$

4) Изменение площади $A$ кольца с изменением $x$:

Мы можем наблюдать, как изменяется площадь кольца в зависимости от ширины внутреннего круга $x$ по таблице. Теперь рассмотрим, как изменяется площадь кольца при различных интервалах изменения $x$:

• От 0 до 2: площадь увеличивается от $0$ до $12 \, \text{см}^2$.
• От 0 до 1: площадь увеличивается от $0$ до $9 \, \text{см}^2$.
• От 1 до 2: площадь увеличивается от $9 \, \text{см}^2$ до $12 \, \text{см}^2$.

Каждое из этих изменений можно наблюдать в графике, который представляет собой параболу, открывающуюся вверх.