ГДЗ по Алгебре 9 Класс Номер 277 Дорофеев, Суворова — Подробные Ответы

1) Запишите уравнение, описывающее высоту, на которой находится мяч, в зависимости от времени полета (рост футболиста считайте равным 2 м).

2) Начертите график зависимости высоты от времени.

3) Определите по графику:
а) на какую максимальную высоту поднимется мяч;
б) через сколько примерно времени мяч окажется на максимальной высоте;
в) когда скорость полета мяча больше: в начале или в конце первой секунды движения;
г) через сколько примерно секунд мяч упадет на землю.

В задачах 278–279 воспользуйтесь формулой площади круга $S = \pi r^2$, где $r$ — радиус круга, $\pi \approx 3$.

$h_0 = 2 \, \text{м}$ — рост футболиста (начальная высота);
$v_0 = 10 \, \text{м/с}$ — начальная скорость мяча;
$g = 9.8 \, \text{м/с}^2$ — ускорение свободного падения;

1) Уравнение зависимости высоты $h$ мяча от времени $t$ полета:

$$h = -\frac{1}{2}gt^2 + v_0t + h_0;$$ $$h = -\frac{1}{2} \cdot 9.8 \cdot t^2 + 10 \cdot t + 2;$$ $$h = -4.9t^2 + 10t + 2;$$

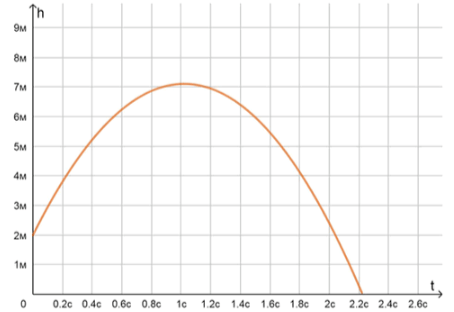
2) График зависимости высоты от времени полета:

$$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline t & 0,4 & 0,8 & 1 & 1,2 & 1,4 & 1,8 & 2 & 2,2 \\ \hline h & 5,2 & 6,8 & 7,1 & 6,9 & 6,4 & 4,1 & 2,4 & 0,3 \\ \hline \end{array}$$

3) Определим по графику:
а) Максимальная высота подъема мяча — около 7 метров;
б) Мяч окажется на этой высоте приблизительно через 1 секунду;
в) Скорость мяча больше в начале первой секунды;
г) Мяч упадет на землю приблизительно через 2,2 секунды.

1) Уравнение зависимости высоты $h$ мяча от времени $t$ полета:

Мы знаем, что высота мяча изменяется в зависимости от времени падения, а его движение подчиняется законам механики, то есть оно является результатом действия силы тяжести. Исходя из этого, можем записать уравнение движения мяча с учетом начальных данных:

$$h = -\frac{1}{2} g t^2 + v_0 t + h_0$$

где:

• $g = 9,8 \, \text{м/с}^2$ — ускорение свободного падения;
• $v_0 = 10 \, \text{м/с}$ — начальная скорость мяча;
• $h_0 = 2 \, \text{м}$ — начальная высота мяча (поскольку рост футболиста равен 2 м).

Подставляем эти значения в уравнение:

$$h = -\frac{1}{2} \cdot 9,8 \cdot t^2 + 10 \cdot t + 2$$

Рассчитаем каждое из слагаемых:

• $-\frac{1}{2} \cdot 9,8 = -4,9$, и у нас получается:

$$h = -4,9 t^2 + 10 t + 2$$

Таким образом, уравнение зависимости высоты мяча от времени полета имеет вид:

$$h = -4,9 t^2 + 10 t + 2$$

Это уравнение выражает зависимость высоты мяча от времени его полета. Парабола, описывающая движение мяча, имеет открытие вниз, так как коэффициент при $t^2$ отрицателен.

2) График зависимости высоты от времени полета:

Для построения графика функции $h(t)$ подставим разные значения $t$ в уравнение и получим соответствующие значения высоты $h$. Например, вычислим значения функции для следующих значений времени $t = 0,4; 0,8; 1; 1,2; 1,4; 1,8; 2; 2,2$.

• Для $t = 0,4$:

$$h(0,4) = -4,9 \cdot (0,4)^2 + 10 \cdot (0,4) + 2 = -4,9 \cdot 0,16 + 4 + 2 = -0,784 + 4 + 2 = 5,216$$

• Для $t = 0,8$:

$$h(0,8) = -4,9 \cdot (0,8)^2 + 10 \cdot (0,8) + 2 = -4,9 \cdot 0,64 + 8 + 2 = -3,136 + 8 + 2 = 6,864$$

• Для $t = 1$:

$$h(1) = -4,9 \cdot (1)^2 + 10 \cdot (1) + 2 = -4,9 + 10 + 2 = 7,1$$

• Для $t = 1,2$:

$$h(1,2) = -4,9 \cdot (1,2)^2 + 10 \cdot (1,2) + 2 = -4,9 \cdot 1,44 + 12 + 2 = -7,056 + 12 + 2 = 6,944$$

• Для $t = 1,4$:

$$h(1,4) = -4,9 \cdot (1,4)^2 + 10 \cdot (1,4) + 2 = -4,9 \cdot 1,96 + 14 + 2 = -9,604 + 14 + 2 = 6,396$$

• Для $t = 1,8$:

$$h(1,8) = -4,9 \cdot (1,8)^2 + 10 \cdot (1,8) + 2 = -4,9 \cdot 3,24 + 18 + 2 = -15,876 + 18 + 2 = 4,124$$

• Для $t = 2$:

$$h(2) = -4,9 \cdot (2)^2 + 10 \cdot (2) + 2 = -4,9 \cdot 4 + 20 + 2 = -19,6 + 20 + 2 = 2,4$$

• Для $t = 2,2$:

$$h(2,2) = -4,9 \cdot (2,2)^2 + 10 \cdot (2,2) + 2 = -4,9 \cdot 4,84 + 22 + 2 = -23,716 + 22 + 2 = 0,284$$

Теперь соберем эти данные в таблицу:

$$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline t & 0,4 & 0,8 & 1 & 1,2 & 1,4 & 1,8 & 2 & 2,2 \\ \hline h & 5,2 & 6,8 & 7,1 & 6,9 & 6,4 & 4,1 & 2,4 & 0,3 \\ \hline \end{array}$$

Теперь мы можем построить график, отображающий высоту мяча в зависимости от времени полета.

3) Определим по графику:

а) Максимальная высота подъема мяча. Мы видим, что наибольшее значение функции $h(t)$ достигается при $t = 1$, где $h = 7,1 \, \text{м}$. Таким образом, максимальная высота подъема мяча составляет около 7 метров.

б) Через какое время мяч окажется на максимальной высоте. Как мы уже видели, максимальная высота достигается при $t = 1$, следовательно, мяч будет находиться на максимальной высоте примерно через 1 секунду.

в) Когда скорость полета мяча больше: в начале или в конце первой секунды движения. Скорость мяча на первом участке его полета будет больше, так как мяч ускоряется под действием силы тяжести. Следовательно, скорость мяча больше в начале первой секунды, а в дальнейшем она будет уменьшаться по мере подъема, а затем возрастать при падении.

г) Через сколько секунд мяч упадет на землю. Мяч упадет на землю, когда его высота $h = 0$. Мы видим, что при $t = 2,2$ мяч находится на высоте около 0,3 м, что близко к 0. Таким образом, мяч упадет на землю через примерно 2,2 секунды.

Обобщая, можно сказать, что мяч поднимется на максимальную высоту около 7 метров, а затем начнет падать, в течение примерно 2,2 секунд.