Краткий ответ:
а) y = ( x − 1 ) ( x − 5 ) y = (x — 1)(x — 5)
y = x 2 − 5 x − x + 5 ; y = x^2 — 5x — x + 5; y = x 2 − 6 x + 5 ; y = x^2 — 6x + 5;
Координаты вершины параболы:
x = − − 6 2 ⋅ 1 = 6 2 = 3 ;
x = -\frac{-6}{2 \cdot 1} = \frac{6}{2} = 3; y = 4 ⋅ 1 ⋅ 5 − ( − 6 ) 2 4 ⋅ 1 = 20 − 36 4 = − 16 4 = − 4 ; y = \frac{4 \cdot 1 \cdot 5 — (-6)^2}{4 \cdot 1} = \frac{20 — 36}{4} = \frac{-16}{4} = -4;
Координаты некоторых точек:
б) y = ( x + 1 ) ( 2 x − 6 ) y = (x + 1)(2x — 6)
y = 2 x 2 − 6 x + 2 x − 6 ; y = 2x^2 — 6x + 2x — 6; y = 2 x 2 − 4 x − 6 ; y = 2x^2 — 4x — 6;
Координаты вершины параболы:
x = − − 4 2 ⋅ 2 = 4 4 = 1 ;
x = -\frac{-4}{2 \cdot 2} = \frac{4}{4} = 1; y = 4 ⋅ 2 ⋅ ( − 6 ) − ( − 4 ) 2 4 ⋅ 2 = − 48 − 16 8 = − 64 8 = − 8 ; y = \frac{4 \cdot 2 \cdot (-6) — (-4)^2}{4 \cdot 2} = \frac{-48 — 16}{8} = \frac{-64}{8} = -8;
Координаты некоторых точек:
в) y = ( x − 2 ) ( 4 − x ) y = (x — 2)(4 — x)
y = 4 x − x 2 − 8 + 2 x ;
y = 4x — x^2 — 8 + 2x; y = − x 2 + 6 x − 8 ; y = -x^2 + 6x — 8;
Координаты вершины параболы:
x = − 6 2 ⋅ ( − 1 ) = 6 2 = 3 ;
x = -\frac{6}{2 \cdot (-1)} = \frac{6}{2} = 3; y = 4 ⋅ ( − 1 ) ⋅ ( − 8 ) − 6 2 4 ⋅ ( − 1 ) = 32 − 36 − 4 = − 4 − 4 = 1 ; y = \frac{4 \cdot (-1) \cdot (-8) — 6^2}{4 \cdot (-1)} = \frac{32 — 36}{-4} = \frac{-4}{-4} = 1;
Координаты некоторых точек:
г) y = − 0 , 5 x ( 4 + x ) y = -0,5x(4 + x)
y = − 0 , 5 x 2 − 2 x ; y = -0,5x^2 — 2x;
Координаты вершины параболы:
x = − − 2 2 ⋅ ( − 0 , 5 ) = − 2 − 1 = − 2 ;
x = -\frac{-2}{2 \cdot (-0,5)} = \frac{-2}{-1} = -2; y = 4 ⋅ ( − 0 , 5 ) ⋅ 0 − ( − 2 ) 2 4 ⋅ ( − 0 , 5 ) = − 4 − 2 = 2 ; y = \frac{4 \cdot (-0,5) \cdot 0 — (-2)^2}{4 \cdot (-0,5)} = \frac{-4}{-2} = 2;
Координаты некоторых точек:
Подробный ответ:
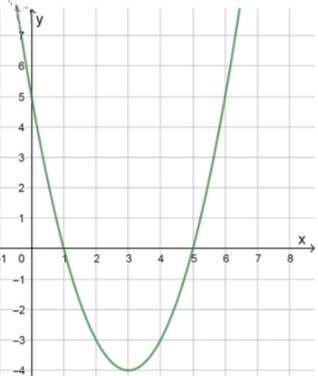
а) y = ( x − 1 ) ( x − 5 ) y = (x — 1)(x — 5)
Раскроем скобки и получим стандартную форму квадратичной функции:
y = ( x − 1 ) ( x − 5 ) = x 2 − 5 x − x + 5 = x 2 − 6 x + 5 y = (x — 1)(x — 5) = x^2 — 5x — x + 5 = x^2 — 6x + 5
Это уравнение имеет вид y = x 2 − 6 x + 5 y = x^2 — 6x + 5
Теперь найдем координаты вершины параболы. Для этого воспользуемся формулой для нахождения абсциссы вершины параболы:
x верш = − b 2 a x_{\text{верш}} = -\frac{b}{2a}
Здесь a = 1 a = 1 b = − 6 b = -6
x верш = − − 6 2 ⋅ 1 = 6 2 = 3 x_{\text{верш}} = -\frac{-6}{2 \cdot 1} = \frac{6}{2} = 3
Теперь находим ординату вершины. Подставим значение x = 3 x = 3
y ( 3 ) = ( 3 ) 2 − 6 ⋅ ( 3 ) + 5 = 9 − 18 + 5 = − 4 y(3) = (3)^2 — 6 \cdot (3) + 5 = 9 — 18 + 5 = -4
Таким образом, вершина параболы находится в точке ( 3 , − 4 ) (3, -4)
Теперь вычислим значения функции в нескольких точках на интервале [ 0 ; 2 ] [0; 2] x = 0 x = 0 x = 1 x = 1 x = 2 x = 2
Для x = 0 x = 0
y ( 0 ) = ( 0 ) 2 − 6 ⋅ ( 0 ) + 5 = 5 y(0) = (0)^2 — 6 \cdot (0) + 5 = 5
Для x = 1 x = 1
y ( 1 ) = ( 1 ) 2 − 6 ⋅ ( 1 ) + 5 = 1 − 6 + 5 = 0 y(1) = (1)^2 — 6 \cdot (1) + 5 = 1 — 6 + 5 = 0
Для x = 2 x = 2
y ( 2 ) = ( 2 ) 2 − 6 ⋅ ( 2 ) + 5 = 4 − 12 + 5 = − 3 y(2) = (2)^2 — 6 \cdot (2) + 5 = 4 — 12 + 5 = -3
Теперь соберем координаты точек в таблицу:
x 0 1 2 y 5 0 − 3 \begin{array}{|c|c|c|c|c|} \hline x & 0 & 1 & 2 \\ \hline y & 5 & 0 & -3 \\ \hline \end{array}
Наибольшее значение функции на интервале [ 0 ; 2 ] [0; 2] y max = 5 y_{\text{max}} = 5 y min = − 4 y_{\text{min}} = -4
Область значений функции: E ( f ) = [ − 4 ; 5 ] E(f) = [-4; 5]
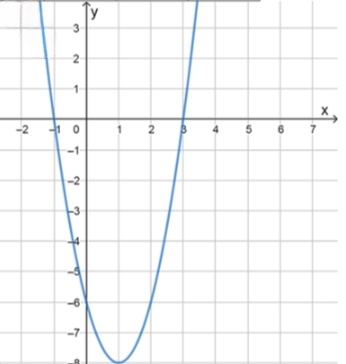
б) y = ( x + 1 ) ( 2 x − 6 ) y = (x + 1)(2x — 6)
Раскроем скобки и получим стандартную форму:
y = ( x + 1 ) ( 2 x − 6 ) = x ( 2 x − 6 ) + 1 ( 2 x − 6 ) = 2 x 2 − 6 x + 2 x − 6 = 2 x 2 − 4 x − 6 y = (x + 1)(2x — 6) = x(2x — 6) + 1(2x — 6) = 2x^2 — 6x + 2x — 6 = 2x^2 — 4x — 6
Теперь находим координаты вершины параболы. Используем формулу для нахождения абсциссы вершины:
x верш = − b 2 a x_{\text{верш}} = -\frac{b}{2a}
Здесь a = 2 a = 2 b = − 4 b = -4
x верш = − − 4 2 ⋅ 2 = 4 4 = 1 x_{\text{верш}} = -\frac{-4}{2 \cdot 2} = \frac{4}{4} = 1
Теперь вычислим ординату вершины. Подставляем x = 1 x = 1
y ( 1 ) = 2 ⋅ ( 1 ) 2 − 4 ⋅ ( 1 ) − 6 = 2 − 4 − 6 = − 8 y(1) = 2 \cdot (1)^2 — 4 \cdot (1) — 6 = 2 — 4 — 6 = -8
Таким образом, вершина параболы находится в точке ( 1 , − 8 ) (1, -8)
Теперь вычислим значения функции в нескольких точках на интервале [ − 1 ; 2 ] [-1; 2]
Для x = − 1 x = -1
y ( − 1 ) = 2 ⋅ ( − 1 ) 2 − 4 ⋅ ( − 1 ) − 6 = 2 + 4 − 6 = 0 y(-1) = 2 \cdot (-1)^2 — 4 \cdot (-1) — 6 = 2 + 4 — 6 = 0
Для x = 0 x = 0
y ( 0 ) = 2 ⋅ ( 0 ) 2 − 4 ⋅ ( 0 ) − 6 = − 6 y(0) = 2 \cdot (0)^2 — 4 \cdot (0) — 6 = -6
Для x = 2 x = 2
y ( 2 ) = 2 ⋅ ( 2 ) 2 − 4 ⋅ ( 2 ) − 6 = 8 − 8 − 6 = − 6 y(2) = 2 \cdot (2)^2 — 4 \cdot (2) — 6 = 8 — 8 — 6 = -6
Соберем координаты точек в таблицу:
x − 1 0 2 y 0 − 6 − 6 \begin{array}{|c|c|c|c|} \hline x & -1 & 0 & 2 \\ \hline y & 0 & -6 & -6 \\ \hline \end{array}
Наибольшее значение функции на интервале [ − 1 ; 2 ] [-1; 2] y max = 0 y_{\text{max}} = 0 y min = − 8 y_{\text{min}} = -8
Область значений функции: E ( f ) = [ − 8 ; 0 ] E(f) = [-8; 0]
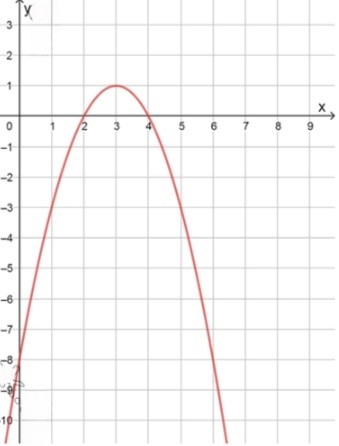
в) y = ( x − 2 ) ( 4 − x ) y = (x — 2)(4 — x)
Раскроем скобки:
y = ( x − 2 ) ( 4 − x ) = x ( 4 − x ) − 2 ( 4 − x ) = 4 x − x 2 − 8 + 2 x = − x 2 + 6 x − 8 y = (x — 2)(4 — x) = x(4 — x) — 2(4 — x) = 4x — x^2 — 8 + 2x = -x^2 + 6x — 8
Теперь находим координаты вершины параболы. Используем формулу для нахождения абсциссы вершины:
x верш = − b 2 a x_{\text{верш}} = -\frac{b}{2a}
Здесь a = − 1 a = -1 b = 6 b = 6
x верш = − 6 2 ⋅ ( − 1 ) = 6 2 = 3 x_{\text{верш}} = -\frac{6}{2 \cdot (-1)} = \frac{6}{2} = 3
Теперь вычислим ординату вершины. Подставляем x = 3 x = 3
y ( 3 ) = − ( 3 ) 2 + 6 ⋅ ( 3 ) − 8 = − 9 + 18 − 8 = 1 y(3) = -(3)^2 + 6 \cdot (3) — 8 = -9 + 18 — 8 = 1
Таким образом, вершина параболы находится в точке ( 3 , 1 ) (3, 1)
Теперь вычислим значения функции в нескольких точках на интервале [ 0 ; 6 ] [0; 6]
Для x = 0 x = 0
y ( 0 ) = − ( 0 ) 2 + 6 ⋅ ( 0 ) − 8 = − 8 y(0) = -(0)^2 + 6 \cdot (0) — 8 = -8
Для x = 1 x = 1
y ( 1 ) = − ( 1 ) 2 + 6 ⋅ ( 1 ) − 8 = − 1 + 6 − 8 = − 3 y(1) = -(1)^2 + 6 \cdot (1) — 8 = -1 + 6 — 8 = -3
Для x = 2 x = 2
y ( 2 ) = − ( 2 ) 2 + 6 ⋅ ( 2 ) − 8 = − 4 + 12 − 8 = 0 y(2) = -(2)^2 + 6 \cdot (2) — 8 = -4 + 12 — 8 = 0
Соберем координаты точек в таблицу:
x 0 1 2 4 5 6 y − 8 − 3 0 0 − 3 − 8 \begin{array}{|c|c|c|c|c|c|} \hline x & 0 & 1 & 2 & 4 & 5 & 6 \\ \hline y & -8 & -3 & 0 & 0 & -3 & -8 \\ \hline \end{array}
Наибольшее значение функции на интервале [ 0 ; 6 ] [0; 6] y max = 1 y_{\text{max}} = 1 y min = − 8 y_{\text{min}} = -8
Область значений функции: E ( f ) = [ − 8 ; 1 ] E(f) = [-8; 1]
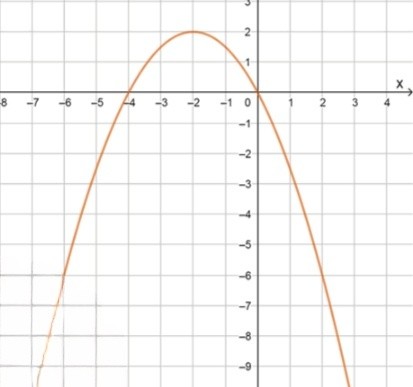
г) y = − 0 , 5 x ( 4 + x ) y = -0,5x(4 + x)
Раскроем скобки:
y = − 0 , 5 x ( 4 + x ) = − 0 , 5 x 2 − 2 x y = -0,5x(4 + x) = -0,5x^2 — 2x
Теперь находим координаты вершины параболы. Используем формулу для нахождения абсциссы вершины:
x верш = − b 2 a x_{\text{верш}} = -\frac{b}{2a}
Здесь a = − 0 , 5 a = -0,5 b = − 2 b = -2
x верш = − − 2 2 ⋅ ( − 0 , 5 ) = − 2 − 1 = − 2 x_{\text{верш}} = -\frac{-2}{2 \cdot (-0,5)} = \frac{-2}{-1} = -2
Теперь вычислим ординату вершины. Подставляем x = − 2 x = -2
y ( − 2 ) = − 0 , 5 ⋅ ( − 2 ) 2 − 2 ⋅ ( − 2 ) = − 0 , 5 ⋅ 4 + 4 = − 2 + 4 = 2 y(-2) = -0,5 \cdot (-2)^2 — 2 \cdot (-2) = -0,5 \cdot 4 + 4 = -2 + 4 = 2
Таким образом, вершина параболы находится в точке ( − 2 , 2 ) (-2, 2)
Теперь вычислим значения функции в нескольких точках на интервале [ − 6 ; 2 ] [-6; 2]
Для x = − 6 x = -6
y ( − 6 ) = − 0 , 5 ⋅ ( − 6 ) 2 − 2 ⋅ ( − 6 ) = − 0 , 5 ⋅ 36 + 12 = − 18 + 12 = − 6 y(-6) = -0,5 \cdot (-6)^2 — 2 \cdot (-6) = -0,5 \cdot 36 + 12 = -18 + 12 = -6
Для x = − 4 x = -4
y ( − 4 ) = − 0 , 5 ⋅ ( − 4 ) 2 − 2 ⋅ ( − 4 ) = − 0 , 5 ⋅ 16 + 8 = − 8 + 8 = 0 y(-4) = -0,5 \cdot (-4)^2 — 2 \cdot (-4) = -0,5 \cdot 16 + 8 = -8 + 8 = 0
Для x = 0 x = 0
y ( 0 ) = − 0 , 5 ⋅ ( 0 ) 2 − 2 ⋅ ( 0 ) = 0 y(0) = -0,5 \cdot (0)^2 — 2 \cdot (0) = 0
Для x = 2 x = 2
y ( 2 ) = − 0 , 5 ⋅ ( 2 ) 2 − 2 ⋅ ( 2 ) = − 0 , 5 ⋅ 4 − 4 = − 2 − 4 = − 6 y(2) = -0,5 \cdot (2)^2 — 2 \cdot (2) = -0,5 \cdot 4 — 4 = -2 — 4 = -6
Соберем координаты точек в таблицу:
x − 6 − 4 0 2 y − 6 0 0 − 6 \begin{array}{|c|c|c|c|c|} \hline x & -6 & -4 & 0 & 2 \\ \hline y & -6 & 0 & 0 & -6 \\ \hline \end{array}
Наибольшее значение функции на интервале [ − 6 ; 2 ] [-6; 2] y max = 2 y_{\text{max}} = 2 y min = − 6 y_{\text{min}} = -6
Область значений функции: E ( f ) = [ − 6 ; 2 ] E(f) = [-6; 2]





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!