
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 271 Дорофеев, Суворова — Подробные Ответы
а) ;
б) ;
в) ;
г) ;
д) .
В каждом случае укажите:
1) промежутки возрастания и убывания функции;
2) значения , при которых ; ; ;
3) наибольшее или наименьшее значение функции;
4) область значений функции.
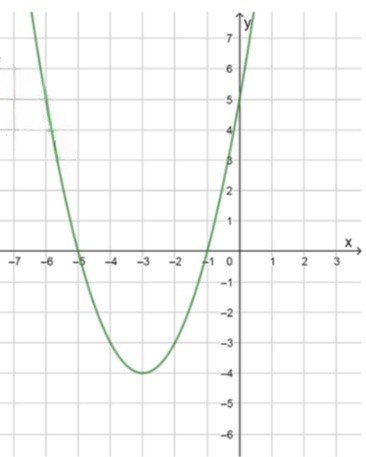
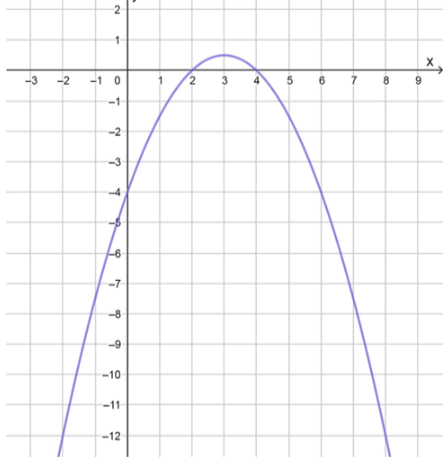
а) :
Координаты вершины параболы:
Координаты некоторых точек:
1) Функция возрастает при ;
Функция убывает при ;
при и ;
при ;
при ;
3) Наименьшее значение: ;
4) Область значений: .
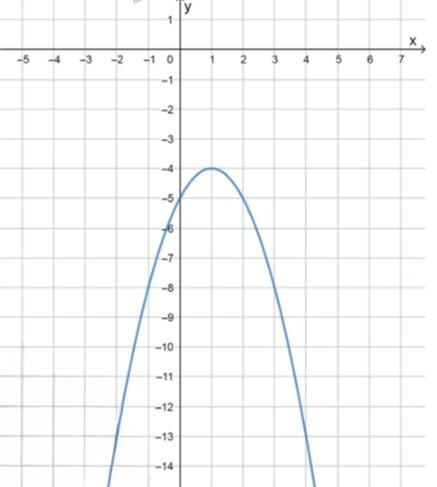
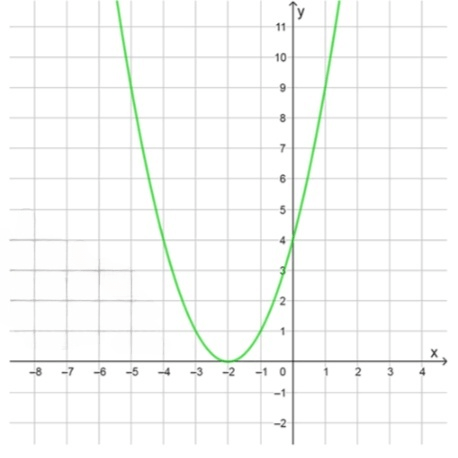
б) :
Координаты вершины параболы:
Координаты некоторых точек:
1) Функция возрастает при ;
Функция убывает при ;
при ;
3) Наибольшее значение: ;
4) Область значений: .
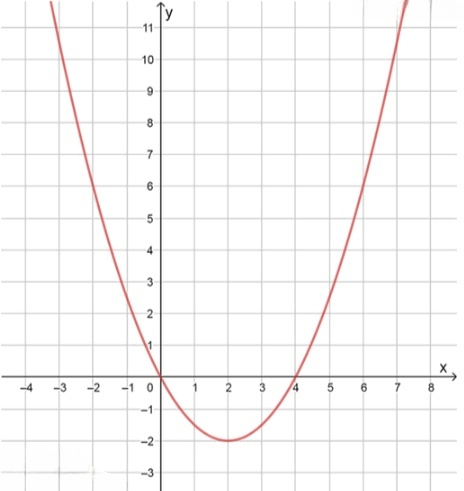
в) :
Координаты вершины параболы:
Координаты некоторых точек:
1) Функция возрастает при ;
Функция убывает при ;
при и ;
при ;
при ;
3) Наименьшее значение: ;
4) Область значений: .
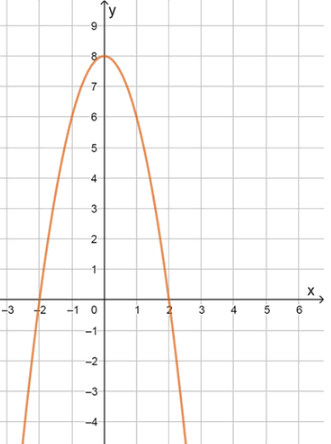
г) :
Координаты вершины параболы:
Координаты некоторых точек:
1) Функция возрастает при ;
Функция убывает при ;
при и ;
при ;
при ;
3) Наибольшее значение: ;
4) Область значений: .
:
Координаты вершины параболы:
Координаты некоторых точек:
1) Функция возрастает при ;
Функция убывает при ;
при и ;
при ;
при ;
3) Наибольшее значение: ;
4) Область значений: ;
:
;
Координаты вершины параболы:
Координаты некоторых точек:
1) Функция возрастает при ;
Функция убывает при ;
при ;
при ;
3) Наименьшее значение: ;
4) Область значений: .
а) :
Для нахождения промежутков возрастания и убывания функции найдем координаты вершины параболы. Для функции вида координата вершины по оси вычисляется по формуле:
В данном случае , . Подставляем эти значения:
Таким образом, вершина параболы находится в точке .
Так как , это значит, что парабола открывается вверх, и функция возрастает после вершины (при ) и убывает до вершины (при ).
Промежутки возрастания и убывания функции:
Функция возрастает при
Функция убывает при
Для нахождения значений , при которых , решим квадратное уравнение:
Вычислим дискриминант:
где , , . Подставляем значения:
Дискриминант положительный, значит у уравнения два действительных корня. Найдем их с помощью формулы для корней квадратного уравнения:
Подставляем значения:
Таким образом, при и .
Для того чтобы найти значения , при которых и , нужно анализировать знаки функции на различных интервалах. Функция имеет положительное значение на промежутках, где она выше оси , и отрицательное значение на промежутках, где она ниже оси .
при
при
Так как вершина параболы имеет значение , это наименьшее значение функции.
Область значений функции:
Поскольку парабола открывается вверх, минимальное значение функции равно , и функция может принимать все значения, начиная с и до бесконечности.
Область значений функции:
б) :
Для нахождения промежутков возрастания и убывания функции найдем координаты вершины параболы. Для функции вида координата вершины по оси вычисляется по формуле:
В данном случае , . Подставляем эти значения:
Таким образом, вершина параболы находится в точке .
Так как , это значит, что парабола открывается вниз, и функция возрастает до вершины (при ) и убывает после вершины (при ).
Промежутки возрастания и убывания функции:
Функция возрастает при
Функция убывает при
Для нахождения значений , при которых , решим квадратное уравнение:
Вычислим дискриминант:
где , , . Подставляем значения:
Так как дискриминант отрицателен, у уравнения нет действительных корней, и график функции не пересекает ось . Таким образом, на всем интервале .
Так как парабола открывается вниз и её максимальное значение достигается в вершине, максимальное значение функции равно .
Область значений функции:
Так как парабола открывается вниз, максимальное значение функции равно , и функция может принимать все значения, меньшие или равные .
Область значений функции:
в) :
Для нахождения промежутков возрастания и убывания функции найдем координаты вершины параболы. Для функции вида координата вершины по оси вычисляется по формуле:
В данном случае , . Подставляем эти значения:
Таким образом, вершина параболы находится в точке .
Так как , это значит, что парабола открывается вверх, и функция возрастает после вершины (при ) и убывает до вершины (при ).
Промежутки возрастания и убывания функции:
Функция возрастает при
Функция убывает при
Для нахождения значений , при которых , решим квадратное уравнение:
Вынесем общий множитель:
Таким образом, или , отсюда .
Таким образом, при и .
Так как парабола открывается вверх, наименьшее значение функции достигается в вершине, где .
Область значений функции:
Так как парабола открывается вверх, минимальное значение функции равно , и функция может принимать все значения, начиная с и до бесконечности.
Область значений функции:
г) :
Для нахождения промежутков возрастания и убывания функции найдем координаты вершины параболы. Для функции вида координата вершины по оси вычисляется по формуле:
В данном случае , . Подставляем эти значения:
Таким образом, вершина параболы находится в точке .
Так как , это значит, что парабола открывается вниз, и функция возрастает до вершины (при ) и убывает после вершины (при ).
Промежутки возрастания и убывания функции:
Функция возрастает при
Функция убывает при
Для нахождения значений , при которых , решим квадратное уравнение:
Переносим 8 на правую сторону:
Делим обе части на :
Извлекаем корень:
Таким образом, при и .
Так как парабола открывается вниз, наибольшее значение функции достигается в вершине, где .
Область значений функции:
Так как парабола открывается вниз, максимальное значение функции равно , и функция может принимать все значения, меньшие или равные .
Область значений функции:
д) :
Для нахождения координат вершины параболы используем формулы для абсциссы вершины:
где и . Подставляем значения:
Таким образом, абсцисса вершины параболы равна .
Теперь находим ординату вершины. Подставляем в исходное уравнение:
Вычислим это поэтапно:
Приводим к общему знаменателю:
Таким образом, ордината вершины .
Координаты вершины параболы: .
Для нахождения значений , при которых , решим уравнение:
Умножим обе части на , чтобы избавиться от дроби:
Вычислим дискриминант для этого уравнения:
где , , . Подставляем значения:
Дискриминант положительный, значит у уравнения два действительных корня. Найдем их с помощью формулы для корней квадратного уравнения:
Подставляем значения:
Таким образом, при и .
Теперь рассмотрим значения функции на интервалах, разделённых этими корнями. Парабола открывается вниз, так как , следовательно, на промежутке между корнями и за пределами этих промежутков.
при
при
Так как парабола открывается вниз, наибольшее значение функции достигается в вершине. Мы уже нашли, что вершина параболы находится в точке .
Область значений функции:
Поскольку парабола открывается вниз, максимальное значение функции равно , и функция может принимать все значения, меньшие или равные .
Область значений функции:
е) :
Для нахождения координат вершины параболы используем формулы для абсциссы вершины:
где , . Подставляем эти значения:
Таким образом, абсцисса вершины параболы равна .
Теперь находим ординату вершины. Подставляем в исходное уравнение:
Вычислим это:
Таким образом, ордината вершины .
Координаты вершины параболы: .
Для нахождения значений , при которых , решим уравнение:
Это уравнение можно представить как полный квадрат:
Таким образом, , отсюда .
Таким образом, при .
Теперь рассмотрим знаки функции:
при
не существует, так как функция всегда неотрицательна.
Так как парабола открывается вверх, минимальное значение функции равно , и оно достигается в вершине.
Область значений функции:
Поскольку парабола открывается вверх, минимальное значение функции равно , и функция может принимать все значения, начиная с и до бесконечности.
Область значений функции:




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!