ГДЗ по Алгебре 9 Класс Номер 269 Дорофеев, Суворова — Подробные Ответы

Функция задана формулой:

$a)$ $y = 2x^2 + 7x + 3$;

$б)$ $y = x^2 — 6x + 11$;

$в)$ $y = -3x^2 + 12x$;

$г)$ $y = -x^2 — 2x — 1$.

В каждом случае выполните следующие задания:

1) Найдите, в какой точке график функции пересекает ось $y$;

2) Определите, пересекает ли график ось $x$, и если да, то в каких точках;

3) Покажите схематическое расположение графика в координатной плоскости.

а) $y = 2x^2 + 7x + 3$:
1) Пересечение с осью $y$ (при $x = 0$):
$y(0) = 2 \cdot 0^2 + 7 \cdot 0 + 3 = 3;$
В точке $(0; 3)$;
2) Пересечение с осью $x$ (при $y = 0$):
$2x^2 + 7x + 3 = 0;$
$D = 7^2 — 4 \cdot 2 \cdot 3 = 49 — 24 = 25, \text{ тогда: }$
$x_1 = \frac{-7 — 5}{2 \cdot 2} = \frac{-12}{4} = -3 \quad \text{и} \quad x_2 = \frac{-7 + 5}{2 \cdot 2} = \frac{-2}{4} = -\frac{1}{2};$
В точках $(-3; 0)$ и $\left(-\frac{1}{2}; 0\right)$;
3) $a = 2 > 0$, значит ветви направлены вверх.

б) $y = x^2 — 6x + 11$:
1) Пересечение с осью $y$ (при $x = 0$):
$y(0) = 0^2 — 6 \cdot 0 + 11 = 11;$
В точке $(0; 11)$;
2) Пересечение с осью $x$ (при $y = 0$):
$x^2 — 6x + 11 = 0;$
$D = 6^2 — 4 \cdot 11 = 36 — 44 = -8;$
$D < 0$, значит таких точек нет;
3) $a = 1 > 0$, значит ветви направлены вверх.

в) $y = -3x^2 + 12x$:
1) Пересечение с осью $y$ (при $x = 0$):
$y(0) = -3 \cdot 0^2 + 12 \cdot 0 = 0;$
В точке $(0; 0)$;
2) Пересечение с осью $x$ (при $y = 0$):
$-3x^2 + 12x = 0 \quad | : (-3);$
$x^2 — 4x = 0;$
$x(x — 4) = 0, \text{ тогда: }$
$x_1 = 0 \quad \text{и} \quad x_2 — 4 = 0, \text{ отсюда } x_2 = 4;$
В точках $(0; 0)$ и $(4; 0)$;
3) $a = -3 < 0$, значит ветви направлены вниз.

г) $y = -x^2 — 2x — 1$:
1) Пересечение с осью $y$ (при $x = 0$):
$y(0) = -0^2 — 2 \cdot 0 — 1 = -1;$
В точке $(0; -1)$;
2) Пересечение с осью $x$ (при $y = 0$):
$-x^2 — 2x — 1 = 0;$
$D = 2^2 — 4 = 4 — 4 = 0, \text{ тогда: }$
$x = \frac{2}{2 \cdot (-1)} = \frac{2}{-2} = -1;$
В точке $(-1; 0)$;
3) $a = -1 < 0$, значит ветви направлены вниз.

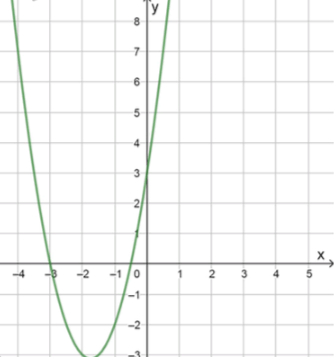
а) $y = 2x^2 + 7x + 3$:

1) Пересечение с осью $y$ (при $x = 0$):
Подставляем $x = 0$ в уравнение функции:

$$y(0) = 2 \cdot 0^2 + 7 \cdot 0 + 3 = 3$$

Таким образом, график функции пересекает ось $y$ в точке $(0; 3)$.

2) Пересечение с осью $x$ (при $y = 0$):
Подставляем $y = 0$ в уравнение функции:

$$2x^2 + 7x + 3 = 0$$

Решим это квадратное уравнение, используя дискриминант.
Дискриминант $D$ вычисляется по формуле:

$$D = b^2 — 4ac$$

где $a = 2$, $b = 7$, $c = 3$.
Подставляем значения:

$$D = 7^2 — 4 \cdot 2 \cdot 3 = 49 — 24 = 25$$

Так как дискриминант положительный, у уравнения есть два корня. Находим их с помощью формулы для корней квадратного уравнения:

$$x_1 = \frac{-b — \sqrt{D}}{2a}, \quad x_2 = \frac{-b + \sqrt{D}}{2a}$$

Подставляем значения:

$$x_1 = \frac{-7 — \sqrt{25}}{2 \cdot 2} = \frac{-7 — 5}{4} = \frac{-12}{4} = -3$$ $$x_2 = \frac{-7 + \sqrt{25}}{2 \cdot 2} = \frac{-7 + 5}{4} = \frac{-2}{4} = -\frac{1}{2}$$

Таким образом, график функции пересекает ось $x$ в точках $(-3; 0)$ и $\left(-\frac{1}{2}; 0\right)$.

3) Так как коэффициент при $x^2$, $a = 2 > 0$, то график функции имеет форму параболы, ветви которой направлены вверх.

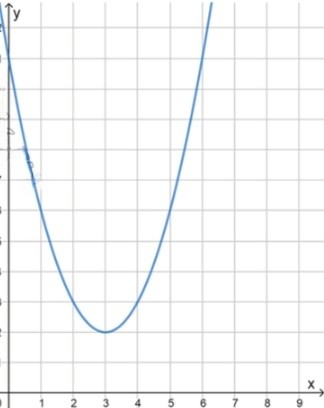
б) $y = x^2 — 6x + 11$:

1) Пересечение с осью $y$ (при $x = 0$):
Подставляем $x = 0$ в уравнение функции:

$$y(0) = 0^2 — 6 \cdot 0 + 11 = 11$$

Таким образом, график функции пересекает ось $y$ в точке $(0; 11)$.

2) Пересечение с осью $x$ (при $y = 0$):
Подставляем $y = 0$ в уравнение функции:

$$x^2 — 6x + 11 = 0$$

Решим это квадратное уравнение, используя дискриминант.
Дискриминант $D$ вычисляется по формуле:

$$D = b^2 — 4ac$$

где $a = 1$, $b = -6$, $c = 11$.
Подставляем значения:

$$D = (-6)^2 — 4 \cdot 1 \cdot 11 = 36 — 44 = -8$$

Так как дискриминант отрицателен, у уравнения нет действительных корней, и график не пересекает ось $x$.

3) Так как коэффициент при $x^2$, $a = 1 > 0$, то график функции имеет форму параболы, ветви которой направлены вверх.

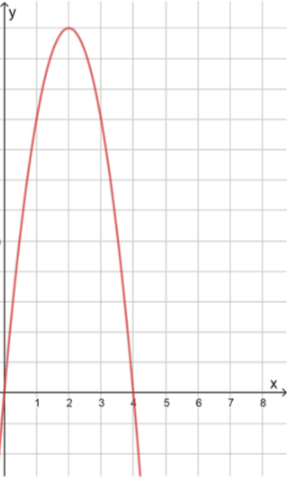
в) $y = -3x^2 + 12x$:

1) Пересечение с осью $y$ (при $x = 0$):
Подставляем $x = 0$ в уравнение функции:

$$y(0) = -3 \cdot 0^2 + 12 \cdot 0 = 0$$

Таким образом, график функции пересекает ось $y$ в точке $(0; 0)$.

2) Пересечение с осью $x$ (при $y = 0$):
Подставляем $y = 0$ в уравнение функции:

$$-3x^2 + 12x = 0$$

Вынесем общий множитель:

$$-3x(x — 4) = 0$$

Таким образом, $x_1 = 0$ и $x_2 = 4$.
График функции пересекает ось $x$ в точках $(0; 0)$ и $(4; 0)$.

3) Так как коэффициент при $x^2$, $a = -3 < 0$, то график функции имеет форму параболы, ветви которой направлены вниз.

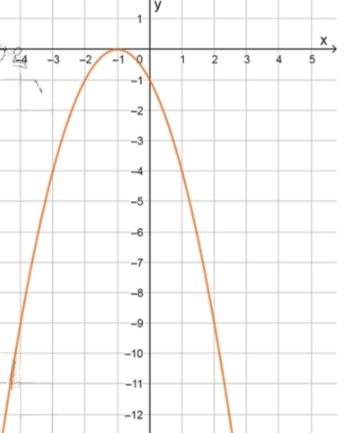
г) $y = -x^2 — 2x — 1$:

1) Пересечение с осью $y$ (при $x = 0$):
Подставляем $x = 0$ в уравнение функции:

$$y(0) = -0^2 — 2 \cdot 0 — 1 = -1$$

Таким образом, график функции пересекает ось $y$ в точке $(0; -1)$.

2) Пересечение с осью $x$ (при $y = 0$):
Подставляем $y = 0$ в уравнение функции:

$$-x^2 — 2x — 1 = 0$$

Решим это квадратное уравнение, используя дискриминант.
Дискриминант $D$ вычисляется по формуле:

$$D = b^2 — 4ac$$

где $a = -1$, $b = -2$, $c = -1$.
Подставляем значения:

$$D = (-2)^2 — 4 \cdot (-1) \cdot (-1) = 4 — 4 = 0$$

Так как дискриминант равен нулю, у уравнения есть один корень. Находим его:

$$x = \frac{-b}{2a} = \frac{-(-2)}{2 \cdot (-1)} = \frac{2}{-2} = -1$$

График функции пересекает ось $x$ в точке $(-1; 0)$.

3) Так как коэффициент при $x^2$, $a = -1 < 0$, то график функции имеет форму параболы, ветви которой направлены вниз.