
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 267 Дорофеев, Суворова — Подробные Ответы
Постройте график функции:
;
;
;
.
В каждом случае укажите нули функции, наименьшее (или наибольшее) значение функции.
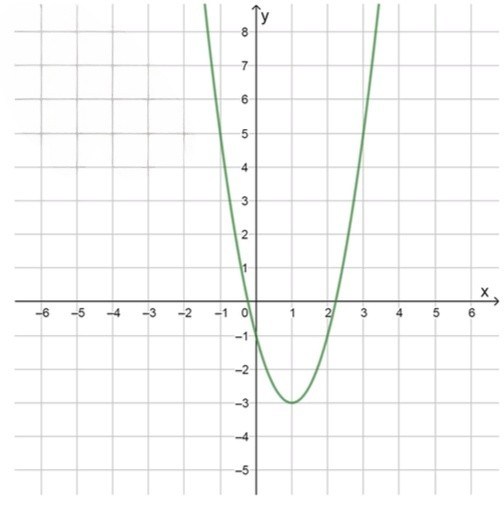
а) :
Координаты вершины параболы:
Координаты некоторых точек:
Нули функции:
Наименьшее значение: ;
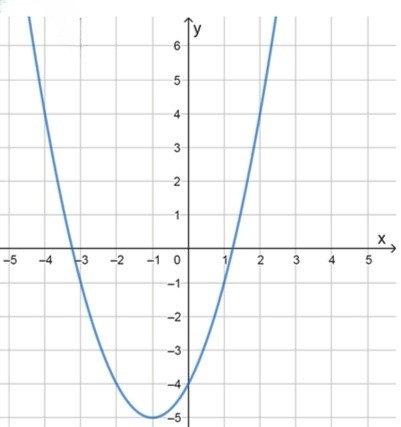
б) :
Координаты вершины параболы:
Координаты некоторых точек:
Нули функции:
Наименьшее значение: ;
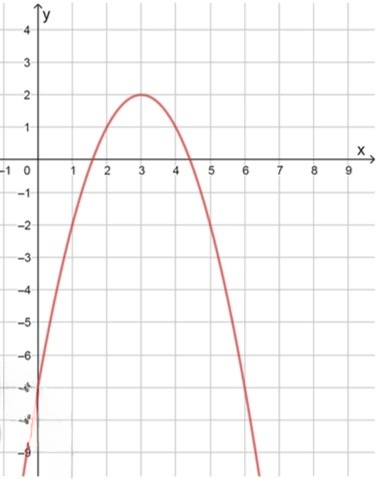
в) :
Координаты вершины параболы:
Координаты некоторых точек:
Нули функции:
Наибольшее значение: ;
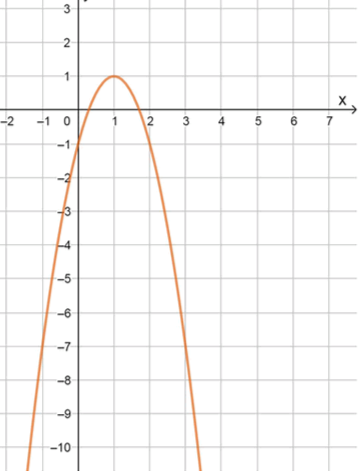
г) :
Координаты вершины параболы:
Координаты некоторых точек:
а) :
Координаты вершины параболы:
Для нахождения абсциссы вершины квадратичной функции используется формула:
Подставляем значения коэффициентов и :
Теперь находим ординату вершины, подставив найденное значение в исходное уравнение:
Таким образом, координаты вершины параболы .
Координаты некоторых точек:
Для вычисления значений функции в разных точках, подставляем соответствующие значения :
- Для :
- Для :
- Для :
- Для :
Таблица значений функции:
Нули функции:
Чтобы найти нули функции, приравниваем :
Для нахождения корней, вычисляем дискриминант :
Таким образом, корни уравнения находятся по формуле:
Следовательно, корни функции:
Наименьшее значение:
Наименьшее значение функции будет на вершине параболы, которое мы вычислили ранее:
б) :
Координаты вершины параболы:
Для нахождения абсциссы вершины используем формулу:
Подставляем значения и :
Теперь находим ординату вершины, подставив в исходное уравнение:
Таким образом, координаты вершины параболы: .
Координаты некоторых точек:
Подставляем различные значения :
- Для :
- Для :
- Для :
- Для :
- Для :
- Для :
Таблица значений функции:
Нули функции:
Для нахождения нулей функции приравниваем её к нулю:
Вычисляем дискриминант :
Тогда корни уравнения:
Корни функции:
Наименьшее значение:
Наименьшее значение функции равно значению в вершине параболы:
в) :
Координаты вершины параболы:
Для нахождения абсциссы вершины используем формулу:
Подставляем значения и :
Находим ординату вершины, подставив в исходное уравнение:
Таким образом, координаты вершины параболы: .
Координаты некоторых точек:
Подставляем разные значения :
- Для :
- Для :
- Для :
- Для :
- Для :
- Для :
Таблица значений функции:
Нули функции:
Для нахождения нулей приравниваем :
Вычисляем дискриминант :
Тогда корни:
Корни:
Наибольшее значение:
Наибольшее значение функции равно значению в вершине параболы:
г) :
Координаты вершины параболы:
Для нахождения абсциссы вершины используем формулу:
Подставляем значения и :
Находим ординату вершины, подставив в исходное уравнение:
Таким образом, координаты вершины параболы: .
Координаты некоторых точек:
Подставляем различные значения :
- Для :
- Для :
- Для :
- Для :
Таблица значений функции:
Нули функции:
Для нахождения нулей приравниваем функцию к нулю:
Вычисляем дискриминант :
Тогда корни уравнения:
Следовательно, корни:
Наибольшее значение:
Наибольшее значение функции будет на вершине параболы, которое мы вычислили ранее:




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!