ГДЗ Дорофеев 9 Класс по Алгебре Шарыгин Учебник 📕 Суворова- Все Части

ГДЗ по Алгебре 9 Класс Номер 264 Дорофеев, Суворова - Подробные Ответы

Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др.

9 класс

Класс

Предмет

ГДЗ Дорофеев 7, 8, 9 Класс по Алгебре Все Учебники - Ответы на Любые Задачи Бесплатно

Тип

ГДЗ, Решебник.

Автор

Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др.

Год

2022.

Издательство

Просвещение.

Описание

Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

ГДЗ по Алгебре 9 Класс Номер 264 Дорофеев, Суворова — Подробные Ответы

Задача

Укажите направление ветвей параболы, вычислите координаты вершины и покажите схематически расположение параболы в координатной плоскости:

а) $y = x^{2} - 4 x + 3$ ;

б) $y = - 2 x^{2} + 2 x - 1$ ;

в) $y = \frac{1}{2} x^{2} + 8 x + 34$ ;

г) $y = - x^{2} - 14 x - 48$ .

Краткий ответ

$y = \frac{4ac — b^2}{4a} = \frac{4 \cdot 1 \cdot 3 — (-4)^2}{4 \cdot 1} = \frac{12 — 16}{4} = \frac{-4}{4} = -1$

У квадратичной функции вида $y = a x^{2} + b x + c$ :

Если $a > 0$ , то ветви параболы направлены вверх;
Если $a < 0$ , то ветви параболы направлены вниз.

Вершина параболы находится в точке $(- \frac{b}{2 a}; \frac{4 a c - b^{2}}{4 a})$ .

а) $y = x^{2} - 4 x + 3$

Направление ветвей:

$a = 1 > 0$ , поэтому ветви параболы направлены вверх.

Координаты вершины:

$x$ -координата вершины:

$x = - \frac{b}{2 a} = - \frac{- 4}{2 \cdot 1} = \frac{4}{2} = 2$

$y$ -координата вершины:

$y = \frac{4 a c - b^{2}}{4 a} = \frac{4 \cdot 1 \cdot 3 - (- 4)^{2}}{4 \cdot 1} = \frac{12 - 16}{4} = \frac{- 4}{4} = - 1$

б) $y = - 2 x^{2} + 2 x - 1$

Направление ветвей:

$a = - 2 < 0$ , поэтому ветви параболы направлены вниз.

Координаты вершины:

$x$ -координата вершины:

$x = - \frac{b}{2 a} = - \frac{2}{2 \cdot (- 2)} = \frac{2}{4} = \frac{1}{2}$

$y$ -координата вершины:

$y = \frac{4 a c - b^{2}}{4 a} = \frac{4 \cdot (- 2) \cdot (- 1) - 2^{2}}{4 \cdot (- 2)} = \frac{8 - 4}{- 8} = \frac{4}{- 8} = - 1$

в) $y = \frac{1}{2} x^{2} + 8 x + 34$

Направление ветвей:

$a = \frac{1}{2} > 0$ , поэтому ветви параболы направлены вверх.

Координаты вершины:

$x$ -координата вершины:

$x = - \frac{b}{2 a} = - \frac{8}{2 \cdot \frac{1}{2}} = - \frac{8}{1} = - 8$

$y$ -координата вершины:

$y = \frac{4 a c - b^{2}}{4 a} = \frac{4 \cdot \frac{1}{2} \cdot 34 - 8^{2}}{4 \cdot \frac{1}{2}} = \frac{68 - 64}{2} = \frac{4}{2} = 2$

$y = \frac{4ac — b^2}{4a} = \frac{4 \cdot (-1) \cdot (-48) — (-14)^2}{4 \cdot (-1)} = \frac{192 — 196}{-4} = \frac{-4}{-4} = 1$

г) $y = - x^{2} - 14 x - 48$

Направление ветвей:

$a = - 1 < 0$ , поэтому ветви параболы направлены вниз.

Координаты вершины:

$x$ -координата вершины:

$x = - \frac{b}{2 a} = - \frac{- 14}{2 \cdot (- 1)} = \frac{14}{- 2} = - 7$

$y$ -координата вершины:

$y = \frac{4 a c - b^{2}}{4 a} = \frac{4 \cdot (- 1) \cdot (- 48) - (- 14)^{2}}{4 \cdot (- 1)} = \frac{192 - 196}{- 4} = \frac{- 4}{- 4} = 1$

Подробный ответ

У квадратичной функции вида $y = a x^{2} + b x + c$ :

Если $a > 0$ , то ветви параболы направлены вверх;
Если $a < 0$ , то ветви параболы направлены вниз.

Вершина параболы находится в точке $(- \frac{b}{2 a}; \frac{4 a c - b^{2}}{4 a})$ .

а) $y = x^{2} - 4 x + 3$

Направление ветвей:

$a = 1 > 0$ , следовательно, ветви параболы направлены вверх.

Координаты вершины:

$x$ -координата вершины:

$x = - \frac{b}{2 a} = - \frac{- 4}{2 \cdot 1} = \frac{4}{2} = 2$

Для вычисления $x$ -координаты вершины, мы используем формулу для координаты $x$ вершины параболы. Подставляем значения $b = - 4$ и $a = 1$ , получаем $x = 2$ .

$y$ -координата вершины:

$y = \frac{4 a c - b^{2}}{4 a} = \frac{4 \cdot 1 \cdot 3 - (- 4)^{2}}{4 \cdot 1} = \frac{12 - 16}{4} = \frac{- 4}{4} = - 1$

Для нахождения $y$ -координаты вершины, подставляем значения $a = 1$ , $b = - 4$ , и $c = 3$ в формулу для $y$ -координаты вершины. После вычислений получаем $y = - 1$ .

б) $y = - 2 x^{2} + 2 x - 1$

Направление ветвей:

$a = - 2 < 0$ , следовательно, ветви параболы направлены вниз.

Координаты вершины:

$x$ -координата вершины:

$x = - \frac{b}{2 a} = - \frac{2}{2 \cdot (- 2)} = \frac{2}{4} = \frac{1}{2}$

Здесь мы подставляем $b = 2$ и $a = - 2$ в формулу для вычисления координаты вершины по оси $x$ . Получаем, что $x = \frac{1}{2}$ .

$y$ -координата вершины:

$y = \frac{4 a c - b^{2}}{4 a} = \frac{4 \cdot (- 2) \cdot (- 1) - 2^{2}}{4 \cdot (- 2)} = \frac{8 - 4}{- 8} = \frac{4}{- 8} = - \frac{1}{2}$

Для нахождения $y$ -координаты вершины, подставляем значения $a = - 2$ , $b = 2$ , и $c = - 1$ в формулу для $y$ . После вычислений получаем $y = - \frac{1}{2}$ .

в) $y = \frac{1}{2} x^{2} + 8 x + 34$

Направление ветвей:

$a = \frac{1}{2} > 0$ , следовательно, ветви параболы направлены вверх.

Координаты вершины:

$x$ -координата вершины:

$x = - \frac{b}{2 a} = - \frac{8}{2 \cdot \frac{1}{2}} = - \frac{8}{1} = - 8$

Подставляем значения $b = 8$ и $a = \frac{1}{2}$ в формулу для вычисления координаты вершины по оси $x$ . После вычислений получаем $x = - 8$ .

$y$ -координата вершины:

$y = \frac{4 a c - b^{2}}{4 a} = \frac{4 \cdot \frac{1}{2} \cdot 34 - 8^{2}}{4 \cdot \frac{1}{2}} = \frac{68 - 64}{2} = \frac{4}{2} = 2$

Для нахождения $y$ -координаты вершины, подставляем значения $a = \frac{1}{2}$ , $b = 8$ , и $c = 34$ в формулу для $y$ . Получаем $y = 2$ .

г) $y = - x^{2} - 14 x - 48$

Направление ветвей:

$a = - 1 < 0$ , следовательно, ветви параболы направлены вниз.

Координаты вершины:

$x$ -координата вершины:

$x = - \frac{b}{2 a} = - \frac{- 14}{2 \cdot (- 1)} = \frac{14}{- 2} = - 7$

Подставляем значения $b = - 14$ и $a = - 1$ в формулу для вычисления координаты вершины по оси $x$ . Получаем $x = - 7$ .

$y$ -координата вершины:

$y = \frac{4 a c - b^{2}}{4 a} = \frac{4 \cdot (- 1) \cdot (- 48) - (- 14)^{2}}{4 \cdot (- 1)} = \frac{192 - 196}{- 4} = \frac{- 4}{- 4} = 1$

Для нахождения $y$ -координаты вершины, подставляем значения $a = - 1$ , $b = - 14$ , и $c = - 48$ в формулу для $y$ . Получаем $y = 1$ .

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

Общая оценка

4.2 / 5

Комментарии

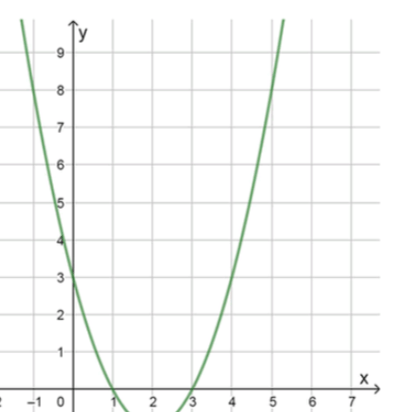
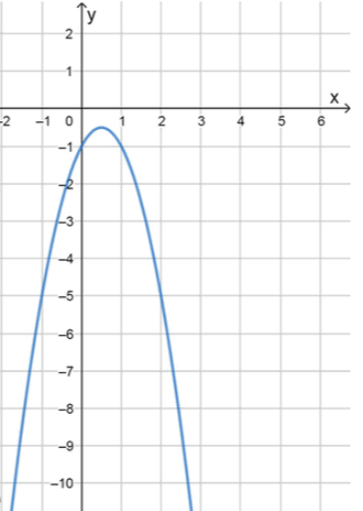
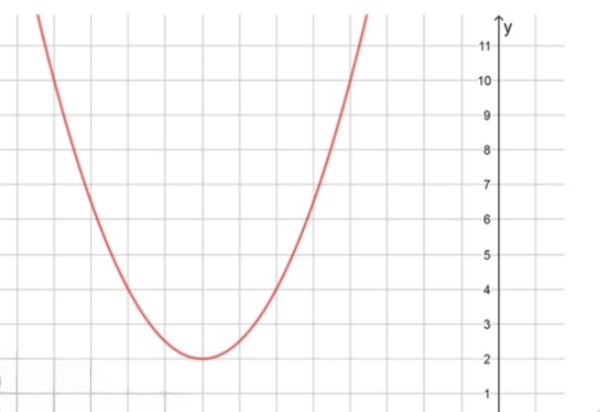
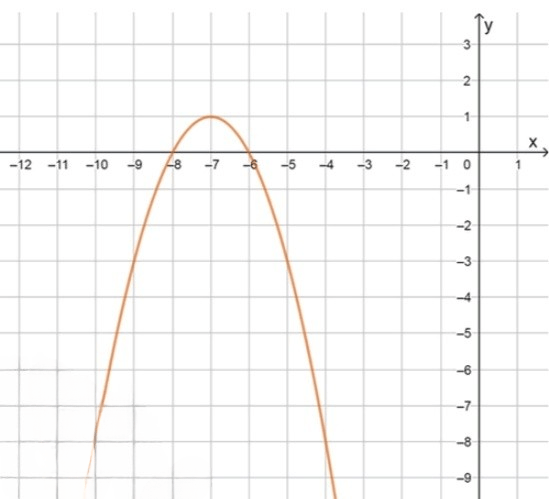
Оставь свой отзыв 💬

Комментариев пока нет, будьте первым!

Другие предметы

ГДЗ Дорофеев 7, 8, 9 Класс по Алгебре Все Учебники - Ответы на Любые Задачи Бесплатно

7-9 класс

7 8 9

ГДЗ Дорофеев 1, 2, 3, 4, 5, 6 Класс по Математике Все Учебники - Ответы на Любые Задачи Бесплатно

1-6 класс

1 2 3 4 5 6