
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 259 Дорофеев, Суворова — Подробные Ответы
В одной системе координат постройте графики функций:
а) , , ;
б) , , ;
в) , , .
График функции получается переносом графика функции на единиц по оси ;
График функции получается переносом графика функции на единиц по оси ;
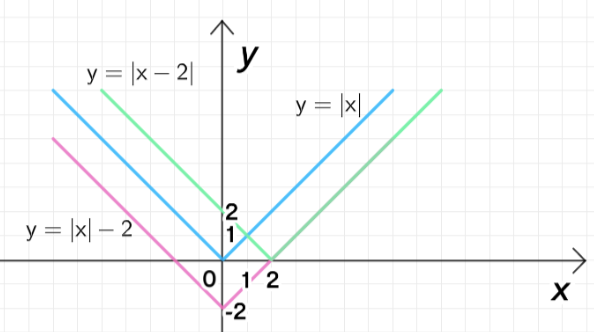
а) , , :
— уравнение графика модуля;
— перенос на 2 единицы вниз;
— перенос на 2 единицы вправо;
б) , , :
— уравнение ветви параболы;
— перенос на 4 единицы вниз;
— перенос на 4 единицы вправо;
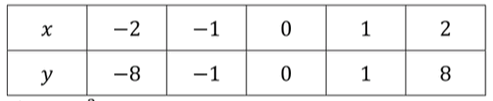
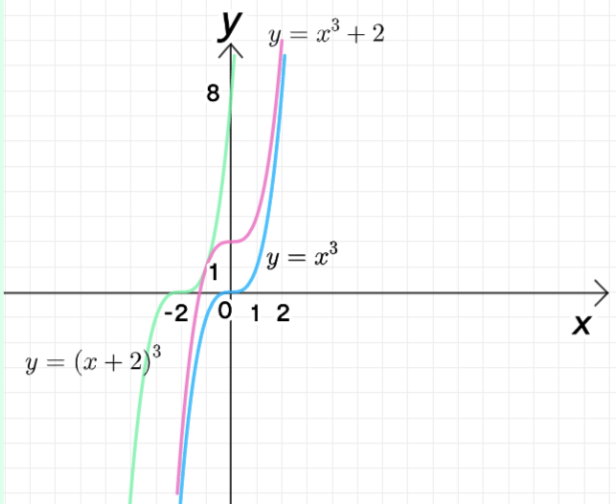
в) , , :
— уравнение кубической параболы;
— перенос на 2 единицы вверх;
— перенос на 2 единицы влево;
График функции получается переносом графика функции на единиц по оси ;
График функции получается переносом графика функции на единиц по оси ;
а) , , :
— это уравнение графика модуля. Парабола, изображённая этим уравнением, открывается вверх, и её вершина находится в точке . График функции представляет собой симметричную относительно оси параболу, которая пересекает ось в точке .
— это уравнение, полученное из функции сдвигом на 2 единицы вниз. Сдвиг вдоль оси происходит за счёт вычитания числа из функции. Такой сдвиг перемещает график вниз, сохраняя его форму. Вершина параболы будет находиться в точке , а ось симметрии останется на месте, то есть вертикальная ось не изменится.
— это уравнение, полученное из функции сдвигом на 2 единицы вправо. В данном случае сдвиг происходит по оси на единицы, так как мы имеем выражение , а не просто . Такой сдвиг изменяет расположение графика, но его форма остаётся прежней. Вершина параболы будет теперь находиться в точке , а ось симметрии перемещается на .
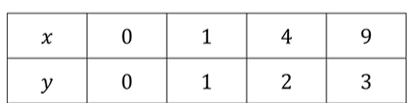
б) , , :
— это уравнение для функции, описывающей верхнюю ветвь параболы, которая начинается в точке и открывается вправо. Функция определена только для , и её график является положительным для всех значений .
в)


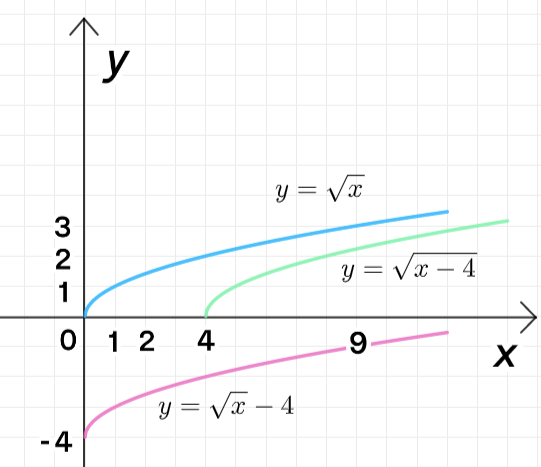


Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!