
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 250 Дорофеев, Суворова — Подробные Ответы
Постройте график функции:
а) ;
б) ;
в) ;
г) .
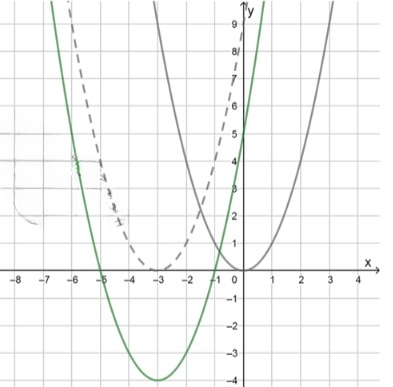
a) :
1) Построим параболу :
2) Перенесем ее на 3 единицы влево;
3) Перенесем, полученный график на 4 единицы вниз;
Функция возрастает на участке ;
Функция убывает на участке ;
Наименьшее значение: .
б) :
1) Построим параболу :

2) Перенесем ее на 1 единицу вправо;
3) Перенесем, полученный график на 3 единицы вверх;
Функция возрастает на участке ;
Функция убывает на участке ;
Наибольшее значение: .
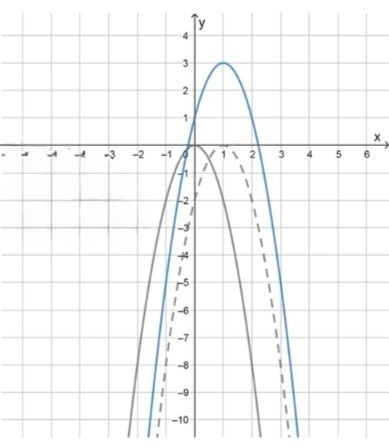
в) :
1) Построим параболу :

2) Перенесем ее на 1 единицу влево;
3) Перенесем, полученный график на 1 единицу вниз;
Функция возрастает на участке ;
Функция убывает на участке ;
Наибольшее значение: .
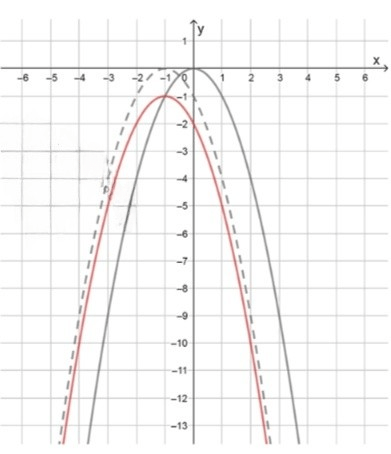
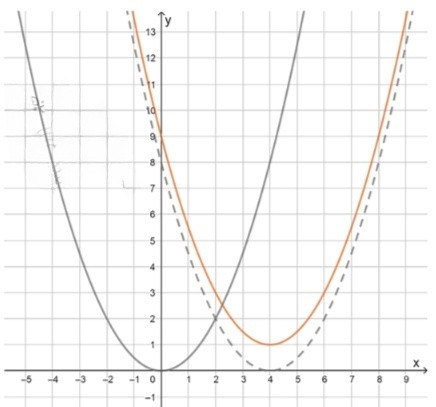
г) :
1) Построим параболу :
2) Перенесем ее на 4 единицы вправо;
3) Перенесем, полученный график на 1 единицу вверх;
Функция возрастает на участке ;
Функция убывает на участке ;
Наименьшее значение: .
a) :
1) Построим параболу :
2) Переносим график на 3 единицы влево. В этом случае, для параболы сдвиг по оси происходит за счет добавления внутри скобок, что изменяет её положение. Вместо точки вершина теперь будет находиться в точке . Парабола сохраняет форму, но перемещается на 3 единицы влево.
3) Переносим полученный график на 4 единицы вниз. Сдвиг на 4 единицы вниз происходит из-за добавления к уравнению, что переносит вершину параболы в точку . Вершина теперь расположена ниже оси .
Функция возрастает на участке ;
Функция убывает на участке ;
Наименьшее значение: .
б) :
1) Построим параболу :
2) Переносим график на 1 единицу вправо. В данном случае, добавление внутри скобок сдвигает график на 1 единицу вправо, меняя положение вершины параболы с на .
3) Переносим полученный график на 3 единицы вверх. Добавление в уравнении сдвигает вершину параболы вверх, в точку .
Функция возрастает на участке ;
Функция убывает на участке ;
Наибольшее значение: .
в) :
1) Построим параболу :

2) Переносим график на 1 единицу влево. В данном случае, внутри скобок сдвигает график на 1 единицу влево. Это приводит к перемещению вершины параболы с точки на .
3) Переносим полученный график на 1 единицу вниз. Добавление в уравнении сдвигает вершину параболы вниз, перемещая её в точку .
Функция возрастает на участке ;
Функция убывает на участке ;
Наибольшее значение: .
г) :
1) Построим параболу :

2) Переносим график на 4 единицы вправо. Парабола сдвигается вправо на 4 единицы, так как у нас выражение , что означает сдвиг на 4 единицы в сторону положительного направления оси , перемещая вершину в точку .
3) Переносим полученный график на 1 единицу вверх. Добавление сдвигает вершину параболы на 1 единицу вверх, так что вершина теперь находится в точке .
Функция возрастает на участке ;
Функция убывает на участке ;
Наименьшее значение: .







Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!