
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 241 Дорофеев, Суворова — Подробные Ответы
С помощью схематического графика определите, имеет ли функция нули, и в случае утвердительного ответа найдите их, решив соответствующее уравнение:
а) ;
б) ;
в) ;
г) .
У функции вида :
Если а, то ветви параболы направлены вверх;
Если а то ветви параболы направлены вниз;
Вершина параболы находится в точке (
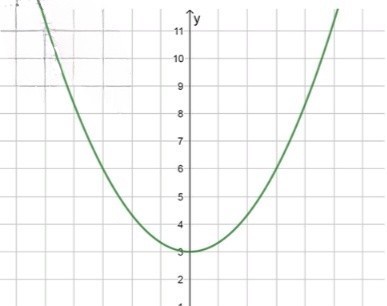
а) :
Ветви параболы направлены вверх, так как ;
Вершина находится в точке , то есть над осью ;
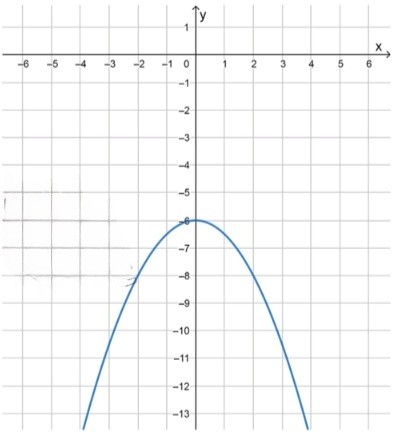
б) :
Ветви параболы направлены вниз, так как ;
Вершина находится в точке , то есть под осью ;
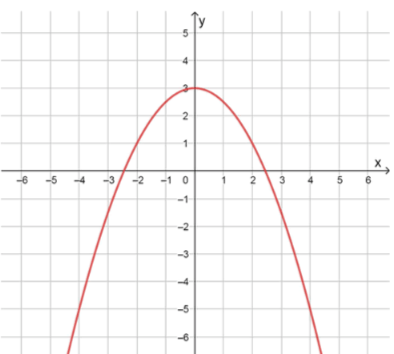
в) :
Ветви параболы направлены вниз, так как ;
Вершина находится в точке , то есть над осью ;
Ответ: .
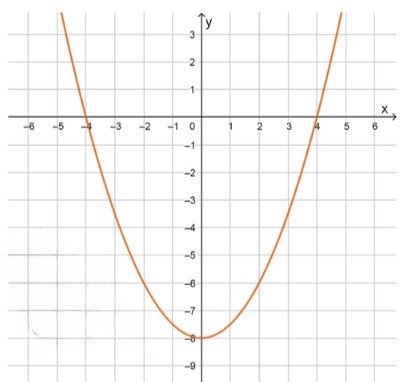
г) :
Ветви параболы направлены вверх, так ка ;
Вершина находится в точке , то есть под осью ;
Ответ: .
У функции вида :
Если , то ветви параболы направлены вверх. Это означает, что график функции будет похож на «U», и вершина параболы будет являться минимальной точкой, то есть все значения функции будут больше или равны , где вершина находится в точке . Таким образом, парабола не пересечет ось , если вершина находится над осью (то есть ). Если меньше нуля, парабола будет пересекать ось , так как для некоторых значений функция примет отрицательные значения.
Если , то ветви параболы направлены вниз. В этом случае парабола будет открываться вниз, и вершина будет максимальной. Это означает, что все значения функции будут меньше или равны , где вершина расположена в точке . Парабола будет пересекать ось , если вершина находится выше оси (то есть ).
Вершина параболы находится в точке . Для всех парабол, заданных уравнением , вершина будет в точке , где является сдвигом вдоль оси . Если , эта точка будет минимальной на графике, а если , то максимальной.
а) :
В данном уравнении , что больше нуля. Это означает, что ветви параболы направлены вверх.
Вершина параболы находится в точке , так как сдвиг по оси равен .
Парабола открывается вверх, и её вершина находится над осью , в точке . Это означает, что функция будет принимать только положительные значения для всех , так как минимальное значение функции будет равно , а все другие значения функции будут больше этого числа.
Таким образом, функция не пересекает ось , так как её минимальное значение больше нуля.
Ответ: не имеет.
б) :
В данном уравнении , что меньше нуля. Это означает, что ветви параболы направлены вниз.
Вершина параболы находится в точке , так как сдвиг по оси равен .
Парабола открывается вниз, и её вершина находится под осью , в точке . Это означает, что функция будет принимать только отрицательные значения для всех , так как максимальное значение функции будет равно , а все другие значения функции будут меньше этого числа.
Таким образом, функция не пересекает ось , так как её максимальное значение меньше нуля.
Ответ: не имеет.
в) :
В данном уравнении , что меньше нуля. Это означает, что ветви параболы направлены вниз.
Вершина параболы находится в точке , так как сдвиг по оси равен .
Парабола открывается вниз, и её вершина находится над осью , в точке . Это означает, что функция будет принимать как положительные, так и отрицательные значения в зависимости от значения .
Для нахождения точек пересечения с осью приравняем к нулю:
Решим это уравнение:
Таким образом, функция пересекает ось в точках .
Ответ:
г) :
В данном уравнении , что больше нуля. Это означает, что ветви параболы направлены вверх.
Вершина параболы находится в точке , так как сдвиг по оси равен .
Парабола открывается вверх, и её вершина находится под осью х, в точке (. Это означает, что функция будет принимать как положительные, так и отрицательные значения в зависимости от значения .
Для нахождения точек пересечения с осью приравняем к нулю:
Решим это уравнение:
Таким образом, функция пересекает ось в точках .
Ответ: .




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!