
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 230 Дорофеев, Суворова — Подробные Ответы
В одной системе координат постройте графики функций:
а) и ;
б) и ;
в) и ;
г) и .
а)
б)
— уравнение параболы:
— уравнение прямой:
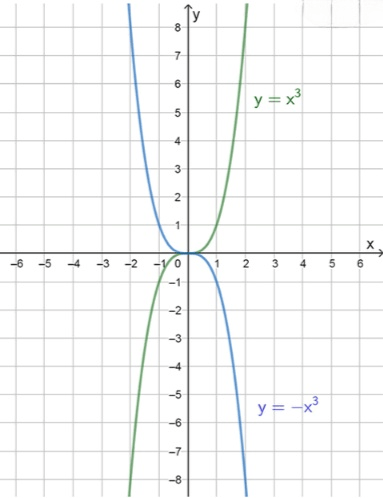
в) и
— уравнение кубической параболы:
— уравнение кубической параболы:
г) и
— уравнение гиперболы в I и III четвертях:
— уравнение гиперболы во II и IV четвертях:
а)
— уравнение прямой:
График функции представляет собой прямую, которая имеет угловой коэффициент . Это означает, что при увеличении , значение уменьшается. Параметр изменяется по оси , а — по оси . Прямая пересекает ось в точке , и её график будет наклонен вниз, с углом наклона 45° по отношению к осям.
Для вычисления значений функции подставим несколько значений :
- При , ,
- При , ,
- При , .
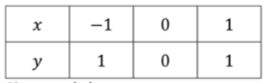
Таблица значений:
— уравнение параболы:
График функции
Для вычисления значений функции подставим несколько значений
- При
x = 1 y = ( 1 ) 2 = 1 - При
x = 2 y = ( 2 ) 2 = 4 - При
x = 3 y = ( 3 ) 2 = 9
Таблица значений:
График функции:
График состоит из двух частей:
- Для
x ≤ 1 y = − x y ( 0 ; 0 ) - Для
x > 1 y = x 2 ( 0 ; 0 )
Таким образом, график функции будет представлять собой разрывную функцию, где для
Ответ: График построен.
б)
График функции
Для вычисления значений функции подставим несколько значений
- При
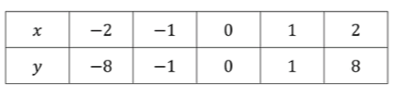
x = − 2 y = − 2 × ( − 2 ) 2 = − 8 - При
x = − 1 y = − 2 × ( − 1 ) 2 = − 2 - При
x = 0 y = − 2 × ( 0 ) 2 = 0
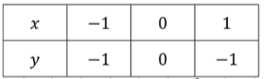
Таблица значений:
График функции
Для вычисления значений функции подставим несколько значений
- При
x = 0 y = − ( 0 ) + 2 = 2 - При
x = 1 y = − ( 1 ) + 2 = 1 - При
x = 2 y = − ( 2 ) + 2 = 0
Таблица значений:
График функции:
График функции состоит из двух частей:
- Для
x < 0 y = − 2 x 2 y ∣ x ∣ - Для
x ≥ 0 y = − x + 2 y ( 0 ; 2 )
Наименьшее значение:
Парабола
Ответ: нет, функция не имеет наименьшего значения.
Наибольшее значение:
Прямая
Ответ: да, функция имеет наибольшее значение, равное
в)
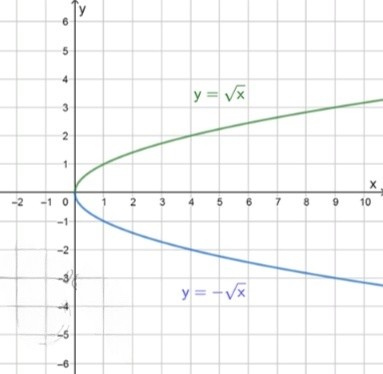
График функции
Для вычисления значений функции подставим несколько значений
- При
x = 0 y = 0 = 0 - При
x = 1 y = 1 = 1 - При
x = 4 y = 4 = 2
Таблица значений:
График функции
Для вычисления значений функции подставим несколько значений
- При
x = 0 y = − 0 = 0 - При
x = 1 y = − 1 = − 1 - При
x = 4 y = − 4 = − 2
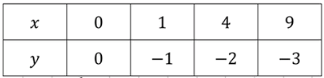
Таблица значений:
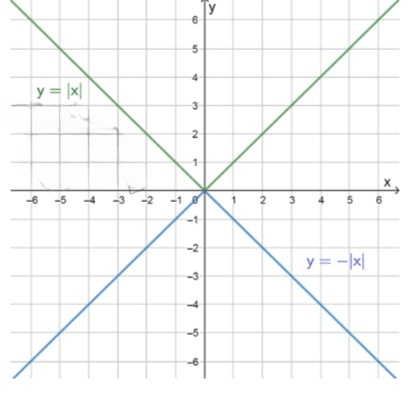
График функции:
График функции состоит из двух частей:
- Для
x ≥ 0 y = x - Для
x ≥ 0 y = − x
Наименьшее значение:
Функция не имеет наименьшего значения, так как
Ответ: нет, функция не имеет наименьшего значения.
Наибольшее значение:
Функция имеет наибольшее значение при
Ответ: да, функция имеет наибольшее значение, равное
г)
График функции
Для вычисления значений функции подставим несколько значений
- При
x = 1 y = 2 1 = 2 - При
x = 2 y = 2 2 = 1 - При
x = 4 y = 2 4 = 0.5
Таблица значений:
График функции
Для вычисления значений функции подставим несколько значений
- При
x = − 1 y = − 2 − 1 = 2 - При
x = − 2 y = − 2 − 2 = 1 - При
x = − 4 y = − 2 − 4 = 0.5
Таблица значений:
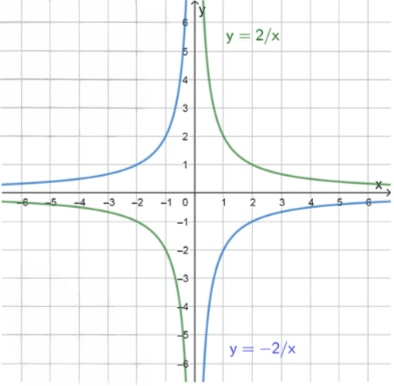
График функции:
График функции состоит из двух гипербол:
- Для
x > 0 y = 2 x - Для
x < 0 y = − 2 x
Наименьшее значение:
Функция не имеет наименьшего значения, так как
Ответ: нет, функция не имеет наименьшего значения.
Наибольшее значение:
Функция не имеет наибольшего значения, так как при
Ответ: нет, функция не имеет наибольшего значения.






Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!