
Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.
ГДЗ по Алгебре 9 Класс Номер 222 Дорофеев, Суворова — Подробные Ответы
В одной системе координат постройте графики функций и найдите координаты их точек пересечения:
а) и ;
б) и ;
в) и ;
г) и .
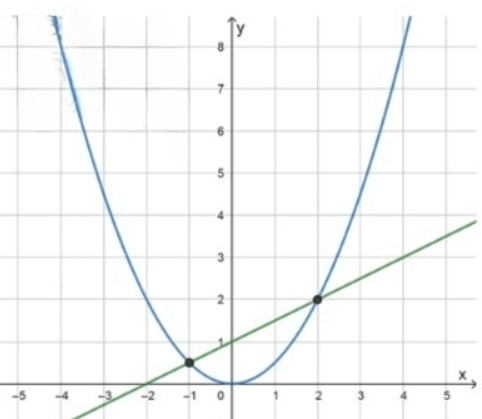
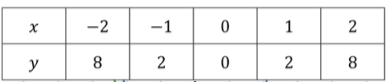
а) и :
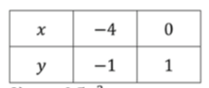
— уравнение прямой:
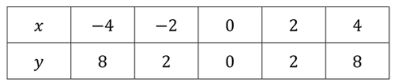
— уравнение параболы:
Точки пересечения: и .
б) и :
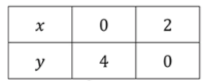
— уравнение прямой:
— уравнение параболы:
Точки пересечения: и .
в) и :
— уравнение гиперболы в I и III четвертях:
— уравнение параболы:
Точка пересечения: .
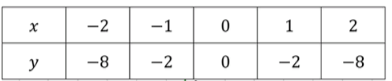
г) и :
— уравнение гиперболы во II и IV четвертях:
— уравнение параболы:
Точка пересечения: .
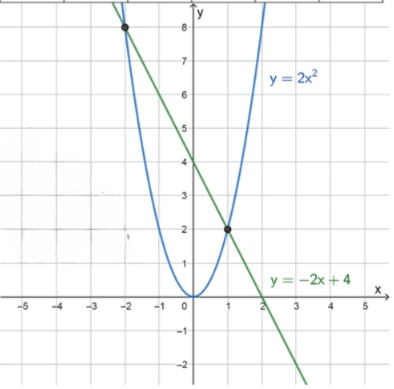
а) и :
— уравнение прямой:
Уравнение прямой имеет вид , где — это угловой коэффициент, а — это свободный член, который указывает на пересечение прямой с осью . Прямая имеет положительный угловой коэффициент, поэтому она будет подниматься слева направо, а её пересечение с осью происходит в точке .
— уравнение параболы:
Уравнение параболы имеет вид , где и . Парабола открывается вверх, так как коэффициент . Вершина параболы находится в точке , и она симметрична относительно оси . Это означает, что при больше или меньше нуля значение функции будет расти.
Для нахождения точек пересечения этих графиков приравняем обе функции:
Переносим все в одну сторону:
Умножим на 2, чтобы избавиться от десятичных:
Решим квадратное уравнение:
Получаем два корня:
Теперь подставим эти значения обратно в уравнение для , чтобы найти координаты точек пересечения:
- Для , .
- Для , .
Точки пересечения: и .
б) и :
— уравнение прямой:
Уравнение прямой имеет вид , где — это угловой коэффициент, а — это свободный член, который указывает на точку пересечения прямой с осью . Эта прямая имеет отрицательный угловой коэффициент, что означает, что она убывает слева направо, а её пересечение с осью происходит в точке .
— уравнение параболы:
Уравнение параболы имеет вид , где и . Парабола открывается вверх, так как коэффициент . Вершина параболы находится в точке , и она симметрична относительно оси .
Для нахождения точек пересечения этих графиков приравняем обе функции:
Переносим все в одну сторону:
Разделим на 2:
Решим квадратное уравнение:
Получаем два корня:
Теперь подставим эти значения обратно в уравнение для , чтобы найти координаты точек пересечения:
- Для , .
- Для , .
Точки пересечения: и .
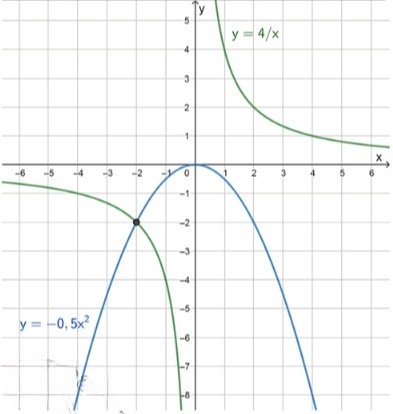
в) и :
— уравнение гиперболы в I и III четвертях:
График функции представляет собой гиперболу, которая имеет асимптоты на осях и . Функция имеет значения, определённые на интервалах и , и график будет располагаться в первой и третьей четвертях.
— уравнение параболы:
Уравнение параболы имеет вид , где и . Парабола открывается вниз, так как коэффициент . Вершина параболы находится в точке , и её ветви направлены вниз.
Для нахождения точек пересечения этих графиков приравняем обе функции:
Умножим обе стороны на , чтобы избавиться от дроби:
Умножим обе стороны на 2:
Извлекаем кубический корень:
Теперь подставим обратно в уравнение для , чтобы найти координату :
Точка пересечения: .
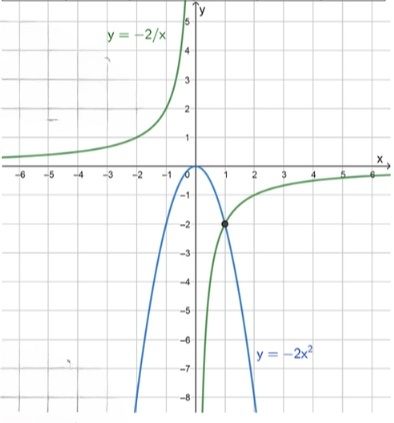
г) и :
— уравнение гиперболы во II и IV четвертях:
График функции представляет собой гиперболу, которая имеет асимптоты на осях и . График будет располагаться во второй и четвёртой четвертях.
— уравнение параболы:
Уравнение параболы имеет вид , где и . Парабола открывается вниз, так как коэффициент .
Для нахождения точек пересечения этих графиков приравняем обе функции:
Умножим обе стороны на :
Разделим обе стороны на -2:
Извлекаем кубический корень:
Теперь подставим обратно в уравнение для , чтобы найти координату :
Точка пересечения: .







Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!