ГДЗ по Алгебре 9 Класс Номер 220 Дорофеев, Суворова — Подробные Ответы

Изобразите в одной и той же системе координат схематически графики функций:

$y = 0.3x^2$, $y = -10x^2$, $y = 8x^2$, $y = -0.1x^2$.

а) Какая из парабол самая «крупная»? самая «плоская»?

б) Какие из функций имеют наименьшее значение? наибольшее значение?

в) Укажите промежуток убывания и промежуток возрастания функций $y = 8x^2$ и $y = -0.1x^2$.

Функции: $y = 0.3x^2$, $y = -10x^2$, $y = 8x^2$, $y = -0.1x^2$;

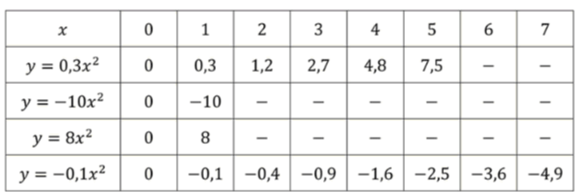
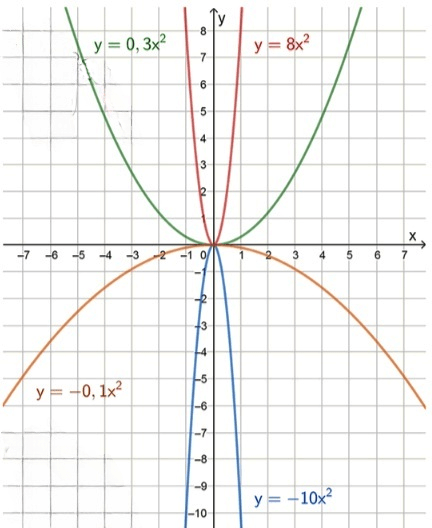
Таблица значений функций и их графики:

а) Самая «крутая» функция: $y = -10x^2$;

Самая «пологая» функция: $y = -0.1x^2$;

б) Наибольшее значение имеют функции: $y = -10x^2$ и $y = -0.1x^2$;

Наименьшее значение имеют функции: $y = 8x^2$ и $y = 0.3x^2$;

в) Функция $y = 8x^2$:

Убывает на участке $x \in (-\infty; 0]$; Возрастает на участке $x \in [0; +\infty)$;

Функция $y = -0.1x^2$:

Убывает на участке $x \in [0; +\infty)$; Возрастает на участке $x \in (-\infty, 0]$.

Функции: $y = 0.3x^2$, $y = -10x^2$, $y = 8x^2$, $y = -0.1x^2$;

Таблица значений функций и их графики:

а) Функция $y = -10x^2$ имеет наибольшее значение по модулю коэффициента перед $x^2$, который равен $-10$. Это означает, что парабола будет самой «крутой», то есть её ветви будут направлены вниз, и график будет более вертикальным.

Это связано с тем, что более высокий по модулю коэффициент приводит к более резкому изменению значения функции при изменении $x$

Функция $y = -0.1x^2$ имеет наименьший по модулю коэффициент перед $x^2$, что делает её параболу самой «пологой». Ветви этой параболы также направлены вниз, но угол наклона будет значительно меньше, чем у параболы функции $y = -10x^2$.

Чем меньше по модулю коэффициент перед $x^2$, тем менее крутой будет график.

б) Функция $y = -10x^2$ имеет наибольшее значение на $x = 0$, так как парабола открывается вниз и вершина параболы является максимальной точкой. В точке вершины $y = 0$.

Для функции $y = -0.1x^2$ также максимальное значение будет в вершине $x = 0$, где значение функции также равно $y = 0$.

Функция $y = 8x^2$ имеет наименьшее значение на $x = 0$, так как парабола открывается вверх и вершина параболы является минимальной точкой. В точке вершины значение функции равно $y = 0$.

Для функции $y = 0.3x^2$также наименьшее значение будет на $x = 0$, и оно будет равно $y = 0$.

в) Функция $y = 8x^2$ открывается вверх, то есть её вершина является точкой минимума. На промежутке $x \in (-\infty; 0]$, когда $x$ уменьшается, функция убывает, так как значения $y$ уменьшаются по мере того, как $x$ приближается к 0.

На промежутке $x \in [0; +\infty)$, когда $x$ увеличивается, функция возрастает, так как значения $y$ увеличиваются.

Функция $y = -0.1x^2$открывается вниз, что означает, что её вершина является точкой максимума. На промежутке $x \in [0; +\infty)$, когда $x$ увеличивается, функция убывает, так как значения $y$ становятся более отрицательными.

На промежутке $x \in (-\infty; 0]$, когда $x$ уменьшается, функция возрастает, так как значения $y$ становятся менее отрицательными и приближаются к 0.