ГДЗ по Алгебре 9 Класс Номер 218 Дорофеев, Суворова — Подробные Ответы

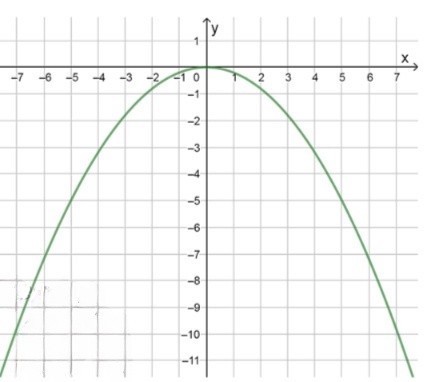
а) Постройте график функции $y = -\frac{1}{5}x^2$.

б) Какие из точек $(10; -20)$, $(-5; -5)$, $\left( \frac{1}{5}; -1 \right)$,$\left( -\frac{1}{2}; -\frac{1}{20} \right)$ принадлежат графику этой функции? Запишите координаты еще каких-либо двух точек, одна из которых принадлежит этому графику, а другая нет.

в) Укажите наибольшее и наименьшее значения этой функции на промежутке $[-2; 6]$, на промежутке $[-5; 5]$.

1) График функции $y = -\frac{1}{5}x^2$:

2) Точки графика:

$$y(10) = -\frac{1}{5} \cdot 10^2 = -\frac{100}{5} = -20;$$

$$y(-5) = -\frac{1}{5} \cdot (-5)^2 = -\frac{25}{5} = -5;$$

$$y\left(\frac{1}{5}\right) = -\frac{1}{5} \cdot \left(\frac{1}{5}\right)^2 = -\frac{1}{5} \cdot \frac{1}{25} = -\frac{1}{125} \neq -1;$$

$$y\left(-\frac{1}{2}\right) = -\frac{1}{5} \cdot \left(-\frac{1}{2}\right)^2 = -\frac{1}{5} \cdot \frac{1}{4} = -\frac{1}{20};$$

Принадлежат точки: $(10; -20)$, $(-5; -5)$$\left(-\frac{1}{2}; -\frac{1}{20}\right)$;

Еще принадлежит точка $\left(3; -\frac{9}{5}\right)$, а не принадлежит точка $(2; -7)$;

3) Значения функции на участках:

На промежутке $[-2; 6]$: $y_{\text{max}} = 0$ и $y_{\text{min}} = -\frac{1}{5} \cdot 6^2 = -\frac{36}{5} = -7,2$;

На промежутке $[-5; 5]$: $y_{\text{max}} = 0$ и $y_{\text{min}} = -5$.

1) График функции $y = -\frac{1}{5}x^2$:

График функции представляет собой параболу, открывающуюся вниз, поскольку коэффициент при $x^2$ отрицателен. Это значит, что при увеличении

$|x|$ значения функции становятся всё более отрицательными, а функция достигает максимума в вершине параболы, где $x = 0$.

2) Точки графика:

Для проверки, принадлежат ли точки графику функции, нужно подставить координаты точек в уравнение функции и убедиться, что значение $y$ совпадает с данным. Для точки $(10; -20)$:

Подставим $x = 10$ в уравнение:

$$y(10) = -\frac{1}{5} \cdot 10^2 = -\frac{1}{5} \cdot 100 = -20$$

Значение функции равно $-20$, следовательно, точка $(10; -20)$ принадлежит графику функции.

Для точки $(-5; -5)$:

Подставим $x = -5$ в уравнение:

$$y(-5) = -\frac{1}{5} \cdot (-5)^2 = -\frac{1}{5} \cdot 25 = -5$$

Значение функции равно $-5$, следовательно, точка $(-5; -5)$ принадлежит графику функции.

Для точки $\left( \frac{1}{5}; -1 \right)$:

Подставим $x = \frac{1}{5}$ в уравнение:

$$y\left( \frac{1}{5} \right) = -\frac{1}{5} \cdot \left( \frac{1}{5} \right)^2 = -\frac{1}{5} \cdot \frac{1}{25} = -\frac{1}{125}$$

Значение функции равно $-\frac{1}{125}$, что не равно $-1$, следовательно, точка $\left( \frac{1}{5}; -1 \right)$ не принадлежит графику функции.

Для точки $\left( -\frac{1}{2}; -\frac{1}{20} \right)$:

Подставим $x = -\frac{1}{2}$ в уравнение:

$$y\left( -\frac{1}{2} \right) = -\frac{1}{5} \cdot \left( -\frac{1}{2} \right)^2 = -\frac{1}{5} \cdot \frac{1}{4} = -\frac{1}{20}$$

Значение функции равно $-\frac{1}{20}$, что совпадает с заданным значением $y$, следовательно, точка $\left( -\frac{1}{2}; -\frac{1}{20} \right)$ принадлежит графику функции.

Теперь укажем еще две точки:

• Точка ($3;-\frac{9}{5}):$

Подставим $x = 3$ в уравнение:

$$y(3) = -\frac{1}{5} \cdot 3^2 = -\frac{1}{5} \cdot 9 = -\frac{9}{5}$$

Значение функции равно $-\frac{9}{5}$, что совпадает с данным значением $y$, следовательно, точка $\left( 3; -\frac{9}{5} \right)$ принадлежит графику функции.

• Точка ($(2; -7)$

Подставим $x = 2$ в уравнение:

$$y(2) = -\frac{1}{5} \cdot 2^2 = -\frac{1}{5} \cdot 4 = -\frac{4}{5}$$

Значение функции равно $-\frac{4}{5}$, что не совпадает с заданным значением $-7$, следовательно, точка $(2; -7)$ не принадлежит графику функции.

3) Значения функции на участках:

Для нахождения наибольшего и наименьшего значений функции на промежутках нужно учитывать, что функция $y = -\frac{1}{5}x^2$является параболой, открывающейся вниз, то есть её максимум будет достигаться в вершине, а минимум на границах промежутка.

• На промежутке [$[-2; 6]$

Максимум функции будет в точке $x = 0$, так как это вершина параболы. Подставим $x = 0$ в уравнение:

$$y(0) = -\frac{1}{5} \cdot 0^2 = 0$$

Таким образом, $y_{\text{max}} = 0$.

Для нахождения минимального значения подставим крайние значения промежутка:

$$y(-2) = -\frac{1}{5} \cdot (-2)^2 = -\frac{1}{5} \cdot 4 = -\frac{4}{5}$$

$$y(6) = -\frac{1}{5} \cdot 6^2 = -\frac{1}{5} \cdot 36 = -\frac{36}{5} = -7,2$$

Минимальное значение на промежутке $[-2; 6]$ будет равно $y_{\text{min}} = -7,2$

• На промежутке [$[-5; 5]$

Максимум функции будет в точке $x = 0$, как и ранее:

$$y(0) = -\frac{1}{5} \cdot 0^2 = 0$$

Таким образом, $y_{\text{max}} = 0$.

Для нахождения минимального значения подставим крайние значения промежутка:

$$y(-5) = -\frac{1}{5} \cdot (-5)^2 = -\frac{1}{5} \cdot 25 = -5$$

$$y(5) = -\frac{1}{5} \cdot 5^2 = -\frac{1}{5} \cdot 25 = -5$$

Минимальное значение на промежутке $[-5; 5]$ будет равно $y_{\text{min}} = -5$.