ГДЗ по Алгебре 9 Класс Номер 213 Дорофеев, Суворова — Подробные Ответы

(Задача-исследование.) Площадь $S$ прямоугольника с периметром, равным 20 см, является функцией длины основания $x$ (рис. 2.8).

1)Задайте функцию $S(x)$ формулой; убедитесь, что это квадратичная функция.

$$S(x)=x(10-x)S(x)=10x-x^2$$

2)Постройте график этой функции.

3)Укажите промежуток, который является областью определения этой функции.

$$0<x<10$$

4)Каковы значения функции в граничных точках области определения? Дайте геометрическое истолкование этого факта.

5)При каком значении длины основания $x$ площадь прямоугольника будет наибольшей? Что это за прямоугольник?
Площадь прямоугольника будет наибольшей, когда $x=5$ см. В этом случае площадь будет равна $25{\text{см}}^2$. Такой прямоугольник является квадратом.

$x$ и $(10 — x)$ — стороны прямоугольника;

$P = 20 \, \text{см}$ — периметр;

1) Функция площади прямоугольника:

$S(x) = x(10 — x)$;

$S(x) = 10x — x^2$;

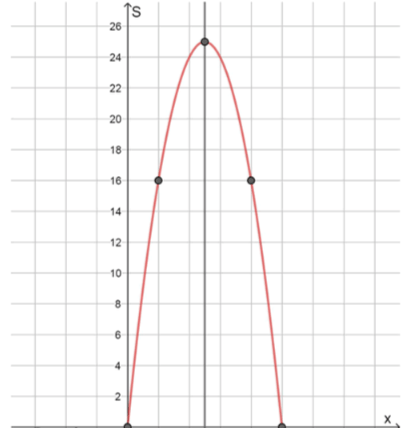
2) Построим график функции:

$10x — x^2 = 0$;

$x(10 — x) = 0$, тогда:

$x_1 = 0$ или $10 — x_2 = 0$, отсюда $x_2 = 10$;

$x = 0$ и $x = 10$ — нули функции;

$x = \frac{0 + 10}{2} = 5$ — ось симметрии;

$S(5) = 10 \cdot 5 — 5^2 = 50 — 25 = 25$;

Вершина параболы — точка $(5; 25)$;

Координаты некоторых других точек:

$S(2) = 10 \cdot 2 — 2^2 = 20 — 4 = 16$;

$S(3) = 10 \cdot 8 — 8^2 = 80 — 64 = 16$;

3) Стороны прямоугольника не могут быть отрицательными, значит:

$\begin{cases} x > 0 \\ 10 — x > 0 \end{cases} \Rightarrow \begin{cases} x > 0 \\ -x > -10 \end{cases} \Rightarrow \begin{cases} x > 0 \\ x < 10 \end{cases};$

$0 < x < 10$;

4) Значения функции в граничных точках области определения:

$S(0) = 10 \cdot 0 — 0^2 = 0$;

$S(10) = 10 \cdot 10 — 10^2 = 100 — 100 = 0$;

В граничных точках одна из сторон прямоугольника равна нулю, то есть он представляет собой отрезок, а площадь отрезка равна нулю;

5) Наибольшая площадь прямоугольника (по графику):

$S_{\text{max}} = 25 \, \text{см}^2$ при $x = 5 \, \text{см}$, тогда $10 — x = 5 \, \text{см}$;

Этот прямоугольник является квадратом.

x и (10 — x) — стороны прямоугольника;
P = 20 см — периметр;

1) Функция площади прямоугольника:
Площадь прямоугольника вычисляется по формуле $S=\text{длина}\times \text{ширина}$. В данном случае длина прямоугольника равна $x$, а ширина — $10-x$, где $x$ — это одна из сторон прямоугольника. Таким образом, функция площади прямоугольника выглядит как:

$$S(x)=x(10-x)$$

Раскрывая скобки, получаем:

$$S(x)=10x-x^2$$

Это квадратичная функция, где коэффициент при $x^2$ отрицателен, что говорит о том, что график функции будет параболой, направленной вниз.

2) Построим график функции:
Чтобы построить график функции, начнем с нахождения корней уравнения $10x-x^2=0$. Для этого решим его:

$$10x-x^2=0$$

Вынесем $x$ за скобки:

$$x(10-x)=0$$

Таким образом, получаем два корня:

$$x_1=0\text{или}{x}_2=10$$

Корни функции $x=0$ и $x=10$ — это точки, в которых площадь прямоугольника равна нулю. Эти значения определяют границы области определения функции.

Нахождение оси симметрии параболы. Осю симметрии для параболы с уравнением вида $a{x}^2+bx+c$ можно найти по формуле:

$$x=\frac{-b}{2a}$$

В нашем случае $a=-1$, $b=10$, так что:

$$x=\frac{-10}{2\times (-1)}=\frac{10}{2}=5$$

Это значит, что ось симметрии графика функции проходит через точку $x=5$.

Теперь подставим $x=5$ в исходную функцию, чтобы найти максимальное значение площади:

$$S(5)=10\cdot 5-5^2=50-25=25$$

Таким образом, наибольшая площадь прямоугольника равна 25 см², и эта площадь достигается, когда одна из сторон прямоугольника равна 5 см, а другая тоже 5 см. Это означает, что при $x=5$ прямоугольник становится квадратом.

Координаты некоторых других точек:
Для нахождения значений функции в других точках подставим различные значения $x$. Например, для $x=2$ и $x=8$:

$$S(2)=10\cdot 2-2^2=20-4=16$$$$S(8)=10\cdot 8-8^2=80-64=16$$

Эти значения показывают, что площадь прямоугольника с такими сторонами равна 16 см².

3) Стороны прямоугольника не могут быть отрицательными, значит:
Мы знаем, что длина сторон прямоугольника не может быть отрицательной. Это означает, что $x>0$ и $10-x>0$. Рассмотрим оба неравенства:

$$x>0\text{и}10-x>0$$

Из второго неравенства $10-x>0$ получаем:

$$x<10$$

Таким образом, $x$ должно быть в интервале:

$$0<x<10$$

Это означает, что возможные значения $x$ должны лежать строго между 0 и 10, чтобы стороны прямоугольника были положительными.

4) Значения функции в граничных точках области определения:
Теперь найдем значения функции на границах области определения, то есть в точках $x=0$ и $x=10$. Подставим эти значения в функцию:

$$S(0)=10\cdot 0-0^2=0$$$$S(10)=10\cdot 10-{10}^2=100-100=0$$

Как видно, при $x=0$ или $x=10$ одна из сторон прямоугольника равна нулю, и площадь прямоугольника становится равной нулю. Это подтверждает, что в этих точках прямоугольник превращается в отрезок.

5) Наибольшая площадь прямоугольника (по графику):
Как мы уже вычислили, максимальная площадь прямоугольника достигается в точке $x=5$. В этой точке стороны прямоугольника равны $5$ см, и площадь равна:

$$S_{\text{max}}=25{\text{см}}^2$$

Этот прямоугольник является квадратом, так как его стороны равны.