ГДЗ Дорофеев 9 Класс по Алгебре Шарыгин Учебник 📕 Суворова- Все Части

ГДЗ по Алгебре 9 Класс Номер 212 Дорофеев, Суворова - Подробные Ответы

Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др.

9 класс

Тип

ГДЗ, Решебник.

Автор

Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б. и др.

Год

2022.

Издательство

Просвещение.

Описание

Учебник по Алгебре для 9-го класса авторов Дорофеева и Суворова — это современное и продуманное пособие, которое помогает школьникам не только освоить базовые математические понятия, но и развить логическое мышление и умение применять знания на практике. Книга построена так, чтобы учебный материал был доступен и интересен даже тем, кто раньше испытывал трудности с математикой.

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

ГДЗ по Алгебре 9 Класс Номер 212 Дорофеев, Суворова — Подробные Ответы

Задача

a) $y = x^{2} + 4 x + 7$ ;
б) $y = - 2 x^{2} + 4 x - 4$ .

При построении пользуйтесь следующим планом:

1) найдите пару симметричных точек параболы, взяв, например, в качестве одной из них точку пересечения с осью $y$ ;

2) далее действуйте по плану, приведенному в упражнении 209, начиная с пункта 2.

Как вы думаете, почему в данном случае первый пункт был заменен? Предложите еще какой-нибудь способ нахождения координат симметричных точек параболы.

Краткий ответ

а) Функция: $y = x^{2} + 4 x + 7$

1) Точка пересечения с осью $y$ ( $x = 0$ ):

$y (0) = 0^{2} + 4 \cdot 0 + 7 = 0 + 7 = 7;$

2) Симметричная точка (точка с такой же ординатой):

$x^{2} + 4 x + 7 = 7;$

$x^{2} + 4 x = 0;$

$x (x + 4) = 0, тогда:$

$x_{1} = 0;$

$x_{2} + 4 = 0, отсюда x_{2} = - 4;$

Точки симметрии $(0; 7)$ и $(- 4; 7)$ ;

3) Ось симметрии равноудалена от точек с равными ординатами:

$x = \frac{0 - 4}{2} = - 2;$

4) Координаты вершины параболы:

$x = - 2 и y (- 2) = (- 2)^{2} + 4 \cdot (- 2) + 7 = 4 - 8 + 7 = 3;$

5) Координаты некоторых других точек:

$y (- 5) = (- 5)^{2} + 4 \cdot (- 5) + 7 = 25 - 20 + 7 = 12;$ $y (- 3) = (- 3)^{2} + 4 \cdot (- 3) + 7 = 9 - 12 + 7 = 4;$ $y (- 1) = (- 1)^{2} + 4 \cdot (- 1) + 7 = 1 - 4 + 7 = 4;$ $y (1) = 1^{2} + 4 \cdot 1 + 7 = 1 + 4 + 7 = 12;$

6) График функции:

б) Функция: $y = - 2 x^{2} + 4 x - 4$

1) Точка пересечения с осью $y$ ( $x = 0$ ):

$y (0) = - 2 \cdot 0^{2} + 4 \cdot 0 - 4 = - 4;$

2) Симметричная точка (точка с такой же ординатой):

$- 2 x^{2} + 4 x - 4 = - 4;$

$- 2 x^{2} + 4 x = 0 ∣ : (- 2);$

$x^{2} - 2 x = 0;$

$x (x - 2) = 0, тогда:$

$x_{1} = 0;$

$x_{2} - 2 = 0, отсюда x_{2} = 2;$

Точки симметрии $(0; - 4)$ и $(2; - 4)$ ;

3) Ось симметрии равноудалена от точек с равными ординатами:

$x = \frac{0 + 2}{2} = 1;$

4) Координаты вершины параболы:

$x = 1 и y (1) = - 2 \cdot 1^{2} + 4 \cdot 1 - 4 = - 2 + 4 - 4 = - 2;$

5) Координаты некоторых других точек:

$y (- 1) = - 2 \cdot (- 1)^{2} + 4 \cdot (- 1) - 4 = - 2 \cdot 1 - 4 - 4 = - 2 - 8 = - 10;$ $y (3) = - 2 \cdot 3^{2} + 4 \cdot 3 - 4 = - 2 \cdot 9 + 12 - 4 = - 18 + 8 = - 10;$

6) График функции:

Первый пункт был заменен, потому что данные функции не имеют нулей.

Для нахождения симметричных точек также можно:

Взять произвольное значение аргумента;
Найти значение функции при этом аргументе;
Найти значение второго аргумента при таком значении функции;
Если второго значения аргумента нет, значит данная точка является вершиной параболы.

вершиной параболы $\boxed{}$

Подробный ответ

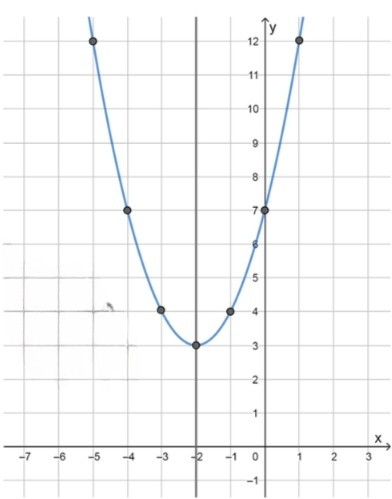
а) Функция: $y = x^{2} + 4 x + 7$

1) Точка пересечения с осью $y$ ( $x = 0$ ):

Для того чтобы найти точку пересечения функции с осью $y$ , нужно подставить $x = 0$ в уравнение функции. Получаем:

$y (0) = 0^{2} + 4 \cdot 0 + 7 = 7.$

Это значит, что точка пересечения функции с осью $y$ имеет координаты $(0, 7)$ .

2) Симметричная точка (точка с такой же ординатой):

Для того чтобы найти вторую точку симметрии, необходимо решить уравнение $x^{2} + 4 x + 7 = 7$ , так как мы ищем точку, где ордината равна 7. Упростим уравнение:

$x^{2} + 4 x = 0,$ $x (x + 4) = 0.$

Решая это уравнение, получаем два корня:

$x_{1} = 0, x_{2} = - 4.$

Таким образом, вторая точка симметрии имеет координаты $(- 4, 7)$ , и обе точки симметрии — $(0, 7)$ и $(- 4, 7)$ .

3) Ось симметрии равноудалена от точек с равными ординатами:

Ось симметрии параболы — это прямая, которая проходит через середину отрезка, соединяющего точки симметрии. Для этого нужно вычислить среднее значение между абсциссами этих точек:

$x = \frac{0 - 4}{2} = - 2.$

Таким образом, ось симметрии параболы — это прямая $x = - 2$ .

4) Координаты вершины параболы:

Вершина параболы находится на оси симметрии, то есть при $x = - 2$ . Подставим это значение в уравнение функции, чтобы найти ординату вершины:

$y (- 2) = (- 2)^{2} + 4 \cdot (- 2) + 7 = 4 - 8 + 7 = 3.$

Таким образом, координаты вершины параболы — $(- 2, 3)$ .

5) Координаты некоторых других точек:

Теперь найдем координаты нескольких других точек функции:

$y (- 5)$ :

$y (- 5) = (- 5)^{2} + 4 \cdot (- 5) + 7 = 25 - 20 + 7 = 12.$

$y (- 3)$ :

$y (- 3) = (- 3)^{2} + 4 \cdot (- 3) + 7 = 9 - 12 + 7 = 4.$

$y (- 1)$ :

$y (- 1) = (- 1)^{2} + 4 \cdot (- 1) + 7 = 1 - 4 + 7 = 4.$

$y (1)$ :

$y (1) = 1^{2} + 4 \cdot 1 + 7 = 1 + 4 + 7 = 12.$

6) График функции:

Теперь, зная координаты точек $(- 5, 12)$ , $(- 3, 4)$ , $(- 1, 4)$ , $(1, 12)$ и вершины $(- 2, 3)$ , можно построить график функции.

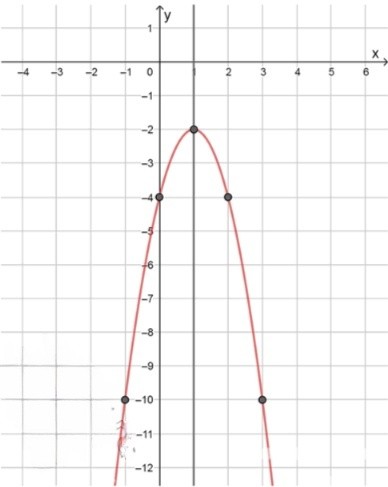
б) Функция: $y = - 2 x^{2} + 4 x - 4$

1) Точка пересечения с осью $y$ ( $x = 0$ ):

Подставим $x = 0$ в уравнение функции:

$y (0) = - 2 \cdot 0^{2} + 4 \cdot 0 - 4 = - 4.$

Точка пересечения функции с осью $y$ имеет координаты $(0, - 4)$ .

2) Симметричная точка (точка с такой же ординатой):

Решим уравнение $- 2 x^{2} + 4 x - 4 = - 4$ :

$- 2 x^{2} + 4 x = 0 ∣ : (- 2),$

$x^{2} - 2 x = 0,$

$x (x - 2) = 0.$

Получаем два корня:

$x_{1} = 0, x_{2} = 2.$

Таким образом, вторая точка симметрии имеет координаты $(2, - 4)$ , и обе точки симметрии — $(0, - 4)$ и $(2, - 4)$ .

3) Ось симметрии равноудалена от точек с равными ординатами:

Ось симметрии параболы проходит через середину отрезка, соединяющего две симметричные точки. Вычислим среднее значение между абсциссами этих точек:

$x = \frac{0 + 2}{2} = 1.$

Таким образом, ось симметрии параболы — это прямая $x = 1$ .

4) Координаты вершины параболы:

Вершина параболы находится на оси симметрии, то есть при $x = 1$ . Подставим это значение в уравнение функции:

$y (1) = - 2 \cdot 1^{2} + 4 \cdot 1 - 4 = - 2 + 4 - 4 = - 2.$

Таким образом, координаты вершины параболы — $(1, - 2)$ .

5) Координаты некоторых других точек:

Теперь найдем координаты нескольких других точек функции:

$y (- 1)$ :

$y (- 1) = - 2 \cdot (- 1)^{2} + 4 \cdot (- 1) - 4 = - 2 - 4 - 4 = - 10.$

$y (3)$ :

$y (3) = - 2 \cdot 3^{2} + 4 \cdot 3 - 4 = - 2 \cdot 9 + 12 - 4 = - 18 + 8 = - 10.$

6) График функции:

Теперь, зная координаты точек $(- 1, - 10)$ , $(3, - 10)$ , и вершины $(1, - 2)$ , можно построить график функции.

Первый пункт был заменен, потому что данные функции не имеют нулей.

Для нахождения симметричных точек также можно:

Взять произвольное значение аргумента;
Найти значение функции при этом аргументе;
Найти значение второго аргумента при таком значении функции;
Если второго значения аргумента нет, значит данная точка является вершиной параболы.

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

Общая оценка

5 / 5

Комментарии

Оставь свой отзыв 💬

Комментариев пока нет, будьте первым!

Другие предметы

ГДЗ Дорофеев 7, 8, 9 Класс по Алгебре Все Учебники - Ответы на Любые Задачи Бесплатно

7-9 класс

7 8 9

ГДЗ Дорофеев 1, 2, 3, 4, 5, 6 Класс по Математике Все Учебники - Ответы на Любые Задачи Бесплатно

1-6 класс

1 2 3 4 5 6